Алгебра: Объясните как решать такие задачи!

olesahshhahas

01.06.2021 22:45

Алгебра

Есть ответ 👍

Объясните как решать такие задачи!

110

212

Посмотреть ответы 3

Ответы на вопрос:

ОСЕНЬ2019

Алгебра

4,5(88 оценок)

2) х ∈ (-∞; 3] ∪[4; +∞)

Объяснение:

Дано неравенство

х² - 7х + 12 ≥ 0

Находим корни уравнения

х² - 7х + 12 = 0

D = 7² - 4 · 12 = 1

х₁ = 0,5 · (7 - 1) = 3

х₂ = 0,5 · (7 + 1) = 4

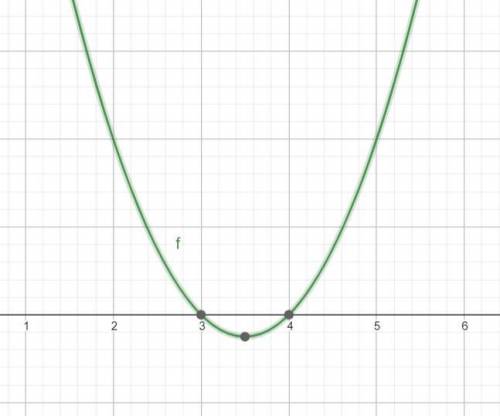
Известно, что графиком функции

y = х² - 7х + 12

является парабола веточками вверх и она пересекает ось Ох в точках

х₁ = 3 и х₂ = 4

Поэтому в интервале между х₁ и х₂ значения функции отрицательны, а на интервалах до х ₁ и после х₂ функция положительна.

Тогда решением неравенства является

х ∈ (-∞; 3] и х ∈ [4; +∞)

Смотрим на рисунки и выбираем то, где заштрихованы это интервалы.

Видим, что это рис.2.

veronikamod

Алгебра

4,7(4 оценок)

Чтобы решить квадратное неравенство, следуйте следующему алгоритму...

Нам дано неравенство: 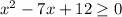$x^{2} -7x+12\geq 0$

1) Записываем в виде функции: 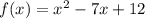$f(x)=x^{2} -7x+12$

2) Ищем нули функции (то есть те точки на оси х, в которых парабола пересекает её). Для этого приравниваем трёхчлен к нулю.

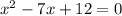
$x^{2} -7x+12=0$

Решаем квадратное уравнение:

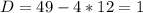
D=49-4*12=1

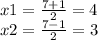
$x1=\frac{7+1}{2}=4\\x2=\frac{7-1}{2}=3$

3) Получившиеся "иксы" - это точки, в которых парабола заныривает под ось Ох. Нам нужно найти промежуток, на котором парабола находится над осью (тк знак 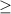$\geq$ ) - смотрите прикреплённый мной рисунок. Парабола имеет положительный коэф-нт k, поэтому ветви вверх. Эту параболу вы должны представить у себя в голове и понять, на каких промежутках ветки находятся в плюсе. То есть над осью х. Это промежутки (-Б;3] и [4;+Б). На промежутке от трёх до четырёх: (3;4) парабола ныряет под ось. То есть там 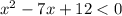$x^{2} -7x+12 < 0$ , а нам нужно 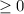$\geq 0$ . Поэтому ответ на чертеже 2.

timbn2006

Алгебра

4,4(9 оценок)

4sin103° * cos103°/ sin206°=2sin206°/sin206°=2

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Алгебра

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.