Регистрация Спросить otvet5GPT
penina1
06.03.2021 03:16
Алгебра
Есть ответ 👍

Четыре числа образуют геометрическую прогрессию. Если к ним прибавить соответственно 4, 6, 6 и 2, то получим четыре числа, которые образуют арифметическую прогрессию. Определи числа, образующие геометрическую прогрессию. q-? b1,b2,b3,b4-?

116
164
Посмотреть ответы 2

Ответы на вопрос:

Franni
Franni
4,8(1 оценок)

Объяснение:

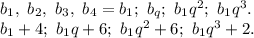
b_1,\ b_2,\ b_3,\ b_4=b_1;\ b_q;\ b_1q^2;\ b_1q^3.\\b_1+4;\ b_1q+6;\ b_1q^2+6;\ b_1q^3+2.

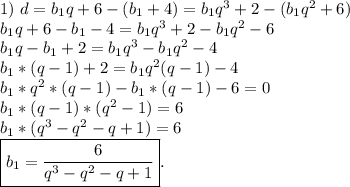
1)\ d=b_1q+6-(b_1+4)=b_1q^3+2-(b_1q^2+6)\\b_1q+6-b_1-4=b_1q^3+2-b_1q^2-6\\b_1q-b_1+2=b_1q^3-b_1q^2-4\\b_1*(q-1)+2=b_1q^2(q-1)-4\\b_1*q^2*(q-1)-b_1*(q-1)-6=0 \\b_1*(q-1)*(q^2-1)=6\\b_1*(q^3-q^2-q+1)=6\\\boxed{b_1=\frac{6}{q^3-q^2-q+1}} .

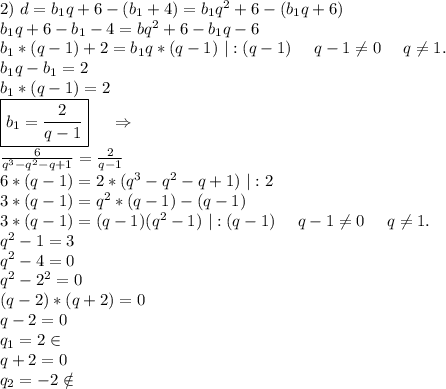
2)\ d=b_1q+6-(b_1+4)=b_1q^2+6-(b_1q+6)\\b_1q+6-b_1-4=bq^2+6-b_1q-6\\b_1*(q-1)+2=b_1q*(q-1)\ |:(q-1)\ \ \ \ q-1\neq 0\ \ \ \ q\neq 1.\\b_1q-b_1=2 \\b_1*(q-1)=2\\\boxed{b_1=\frac{2}{q-1}}\ \ \ \ \Rightarrow\\\frac{6}{q^3-q^2-q+1}=\frac{2}{q-1} \\ 6*(q-1)=2*(q^3-q^2-q+1)\ |:2\\3*(q-1)=q^2*(q-1)-(q-1)\\3*(q-1)=(q-1)(q^2-1)\ |:(q-1)\ \ \ \ q-1\neq 0\ \ \ \ q\neq 1.\\q^2-1=3\\q^2-4=0\\q^2-2^2=0\\(q-2)*(q+2)=0\\q-2=0\\q_1=2\in\\q+2=0\\q_2= -2\notin

q₂≠-2, так как мы не получим арифметическую прогрессию.

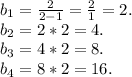
b_1=\frac{2}{2-1}=\frac{2}{1}=2.\\b_2=2*2=4.\\b_3=4*2=8.\\b_4=8*2=16.

ответ: 2; 4; 8; 16.   q=2.

АртурСоколов
АртурСоколов
4,8(70 оценок)
10*(-3)=-30 10x< x потому что -3 ближе к нулю,чем   -30

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS