Регистрация Спросить otvet5GPT
alieismailova1
18.03.2022 07:19
Алгебра
Есть ответ 👍

Cos7x-cos9x+sinx=0
решить уравнение

128
324
Посмотреть ответы 3

Ответы на вопрос:

Zubactick
Zubactick
4,5(29 оценок)

Разность косинусов:

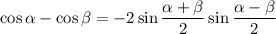
\cos\alpha -\cos\beta =-2\sin\dfrac{\alpha +\beta }{2}\sin \dfrac{\alpha -\beta }{2}

Рассмотрим уравнение:

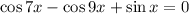
\cos7x-\cos9x+\sin x=0

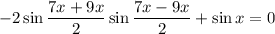
-2\sin\dfrac{7x+9x}{2}\sin\dfrac{7x-9x}{2}+\sin x=0

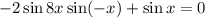
-2\sin8x\sin(-x)+\sin x=0

Учитывая нечетность функции синуса, получим:

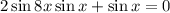
2\sin8x\sin x+\sin x=0

Вынесем общий множитель за скобки:

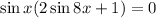
\sin x(2\sin8x+1)=0

Произведение равно нулю когда хотя бы один из множителей равен нулю:

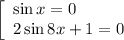
\left[\begin{array}{l} \sin x=0\\ 2\sin8x+1=0\end{array}\right.

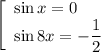
\left[\begin{array}{l} \sin x=0\\ \sin8x=-\dfrac{1}{2} \end{array}\right.

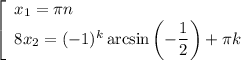
\left[\begin{array}{l} x_1=\pi n\\ 8x_2=(-1)^{k}\arcsin\left(-\dfrac{1}{2}\right)+\pi k \end{array}\right.

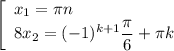
\left[\begin{array}{l} x_1=\pi n\\ 8x_2=(-1)^{k+1}\dfrac{\pi }{6}+\pi k \end{array}\right.

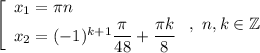
\left[\begin{array}{l} x_1=\pi n\\ x_2=(-1)^{k+1}\dfrac{\pi }{48}+\dfrac{\pi k}{8} \end{array}\right.,\ n,k\in\mathbb{Z}

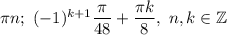
ответ: \pi n;\ (-1)^{k+1}\dfrac{\pi }{48}+\dfrac{\pi k}{8},\ n,k\in\mathbb{Z}

макс3095
макс3095
4,4(88 оценок)

Фото

Объяснение:


Cos7x-cos9x+sinx=0 решить уравнение
МамаВера1
МамаВера1
4,8(13 оценок)
Y=px²-(p+12)x-17 -парабола, х=-1 - ось симметрии параболы, значит абсцисса вершины параболы равна  -1. по формуле абсцисса вершины равна  получаем уравнение, решая которое найдём параметр р:

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS