Регистрация Спросить otvet5GPT
rrjtuk
11.07.2021 08:40
Алгебра
Есть ответ 👍

Пример под цифрами 5.32
! Решите

208
350
Посмотреть ответы 3

Ответы на вопрос:

Keks5478568
Keks5478568
4,8(30 оценок)

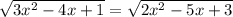
\sqrt{3x^2-4x+1}=\sqrt{2x^2-5x+3}

Правая и левая части равенства неотрицательны, значит можно равенство возвести в квадрат .

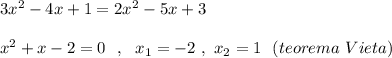
3x^2-4x+1=2x^2-5x+3x^2+x-2=0\ \ ,\ \ x_1=-2\ ,\ x_2=1\ \ (teorema\ Vieta)

Сделаем проверку.

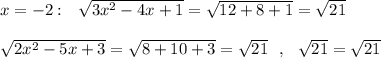x=-2:\ \ \sqrt{3x^2-4x+1}=\sqrt{12+8+1}=\sqrt{21}sqrt{2x^2-5x+3}=\sqrt{8+10+3}=\sqrt{21}\ \ ,\ \ \sqrt{21}=\sqrt{21}     верно

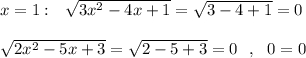x=1:\ \ \sqrt{3x^2-4x+1}=\sqrt{3-4+1}=0sqrt{2x^2-5x+3}=\sqrt{2-5+3}=0\ \ ,\ \ 0=0    верно

ответ: 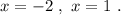 x=-2\ ,\ x=1\ .

anyanaffanya
anyanaffanya
4,4(10 оценок)

Объяснение:

5.32

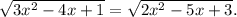
\sqrt{3x^2-4x+1}=\sqrt{2x^2-5x+3} .

ОДЗ:

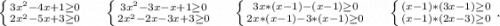
\left \{ {{3x^2-4x+1\geq 0} \atop {2x^2-5x+3\geq 0}} \right. \ \ \ \ \left \{ {{3x^2-3x-x+1\geq 0} \atop {2x^2-2x-3x+3\geq 0}} \right.\ \ \ \ \left \{ {{3x*(x-1)-(x-1)\geq 0} \atop {2x*(x-1)}-3*(x-1)\geq 0} \right.\ \ \ \ \left \{ {{(x-1)*(3x-1)\geq 0} \atop {(x-1)*(2x-3)\geq 0}} \right. .

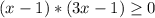
(x-1)*(3x-1)\geq 0\\

(-∞)__+__[1/3]__-__[1]__+__(+∞)              ⇒

x∈(-∞;1/3]U[1;+∞)

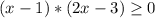
(x-1)*(2x-3)\geq 0\\

(-∞)__+__[1]__-__[1,5]__+__(+∞)        ⇒

x∈(-∞;1]U[1,5;+∞).            ⇒

ОДЗ: x∈(-∞;1/3]U[1]U[1,5;+∞)

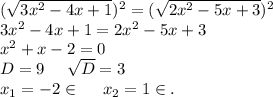
(\sqrt{3x^2-4x+1})^2=(\sqrt{2x^2-5x+3} )^2\\3x^2-4x+1=2x^2-5x+3\\x^2+x-2=0\\D=9\ \ \ \ \sqrt{D}=3\\ x_1=-2\in\ \ \ \ x_2=1\in.

ответ: x₁=-2,  x₂=1.

lilcutthroat
lilcutthroat
4,7(60 оценок)

1)(а+1)(а²-а+1)-а³=а³-а²+а+а²-а+1-а³=1

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS