Геометрия: Если что она лежит на плоскости

leraya08

06.05.2022 14:31

Геометрия

Есть ответ 👍

Если что она лежит на плоскости

147

341

Посмотреть ответы 3

Ответы на вопрос:

irinapak1985

Геометрия

4,5(97 оценок)

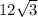
$12 \sqrt{3}$

Объяснение:

1) Т.к. угол CAB=120⁰, а треугольники НАС и НАВ прямоугольные и у них углы НСА и НВА равны 60⁰, то треугольник САВ - равнобедренный и угол АСВ=АВС=(180⁰-120⁰)÷2=60⁰÷2=30⁰.

2) Если в треугольнике САВ провести высоту АН, то получится два равноправных прямоугольных треугольника (СН=НВ).

Из треугольника САН можно найти АН: т.к. уголС=30⁰, то катет лежащий напротив угла 30⁰ равен половине гипотенузы, поэтому АН=1/2×АС=1/2×12=6

по теореме Пифагора найдём СН:

12²=6²+СН²

СН²=12²-6²=144-36=108

СН= корень из 108=6корней из 3

3) ВС=2СН=2×6корней из 3=12корней из 3.

arladich

Геометрия

4,4(42 оценок)

12√3

Объяснение:

1) т.к. АН перпендикулярно плоскости НВС, то АН перпендикулярно НС и НВ(по определению перпендикулярности прямой и плоскости) следовательно, треугольникт АВН и АСН — прямоугольные.

2) Рассмотрим треугольник АНС:

Т.к. сумма острых углов равна 90° в прямоугольном треугольнике, то угол АСН + угол САН = 90°

60°+угол САН=90°

угол САН = 30°. Аналогично, в треугольнике АВН: угол ВАН = 30°(угол АВН + угол ВАН = 90°)

3) АН — общий катет, угол СНА = углу ВАН = 30°, тогда треугольники АНС и АВН равны(по катету и прилежащему острому углу), значит, АС = АВ = 12.

4)Рассмотрим треугольник АВС:

по теореме косинусов: ВС²=АС²+АВ²-2*АВ*АС*cos САВ

х²=12²+12²-2*12*12*cos 120.

x²=2*12²-2*12*12*(-0,5)

x²=2*12²+12²

x²=3*12² → x = 12√3

если вам понравился мой ответ можете поставить пометку «Лучший ответ»?

хлюпхлюпик

Геометрия

4,6(23 оценок)

Имеем : u = угол сав + угол сва = 180 гр - 36 гр = 144 гр сумма углов аве и ваd равна половине суммы u, то есть = 72 гр (так как ad и ве - биссектрисы ). в треугольнике аво угол аов = 180 гр - (угол аво + угол оав) , но угол аво + угол оав = угол аве + угол ваd = 72 гр, поэтому угол аов = 180 гр - 72 гр = 108 гр

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.