Даны вершины треугольника ABC :
A (1;2;3) B(4; -5;4) , C (2; -1;4) .
i) Найдите координаты середины отрезка ВС.
ii) Найдите длину медианы, проведенной из вершины A.

280

476

Посмотреть ответы 2

Ответы на вопрос:

okolota05

Геометрия

4,7(50 оценок)

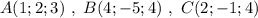
$A(1;2;3)\ ,\ B(4;-5;4)\ ,\ C(2;-1;4)$

1) Пусть точка М - середина отрезка ВC , тогда её координаты вычисляются по формулам

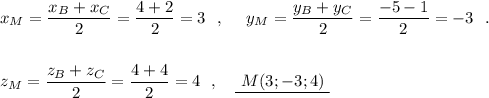
$x_{M}=\dfrac{x_{B}+x_{C}}{2}=\dfrac{4+2}{2}=3\ \ ,\ \ \ \ y_{M}=\dfrac{y_{B}+y_{C}}{2}=\dfrac{-5-1}{2}=-3\ \ .z_{M}=\dfrac{z_{B}+z_{C}}{2}=\dfrac{4+4}{2}=4\ \ ,\ \ \ \underline{\ M(3;-3;4)\ }$

2) Длина медианы АМ .

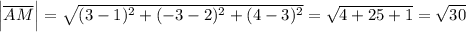
$\Big|\overline{AM}\Big|=\sqrt{(3-1)^2+(-3-2)^2+(4-3)^2}=\sqrt{4+25+1}=\sqrt{30}$

775645

Геометрия

4,4(80 оценок)

точку из которой проведены наклонные обозначим к. опусти из неё на плоскость перпендикуляр кс. точки пересечения наклонных с плоскостью а и в. получим отрезки наклонных ак, вк и их проекции на плоскость ас и вс. треуольники акс и вкс равны как прямоугольные по острому углу и катету (ф и кс). тогда их строны ак и вк равны. обозначим их х. соединим а и в. угол асв по условию равен в. углы кас и квс равны ф. ас=вс=х*cos ф. по теореме косинусов ав квадрат=(х*cos ф)квадрат +(х*cos ф)квадрат -2*х*cos ф*х*cosф*cosв. это в треугольнике асв. в треугольнике акв аналогично ав квадрат=х квадрат+хквадрат-2*х*х* cos k. приравниваем полученные выражения и получим cos k=1-(cos ф)квадрат*(1-cos в). где к искомый угол акв между наклонными

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.