bydarinav2

26.06.2023 13:57

Геометрия

Есть ответ 👍

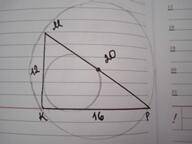
MKP - прямоугольный, K = 90, KM = 12, KP = 16. Найдите радиусы описанной и вписанной окружностей ( Обязательно полное решение с черчением ! )

158

500

Посмотреть ответы 3

Ответы на вопрос:

aydansuper12

Геометрия

4,6(89 оценок)

10 ед, 4 ед.

Объяснение:

Дано: ΔМКР, ∠К=90°, КМ=12, КР=16. R - ?; r - ?

По теореме Пифагора МР=√(КМ²+КР²)=√(144+256)=√400=20.

Радиус описанной окружности равен половине гипотенузы

R=20:2=10.

r=(a+b-c)/2=(12+16-20)/2=8/2=4.

MKP - прямоугольный, K = 90, KM = 12, KP = 16. Найдите радиусы описанной и вписанной окружностей ( О

Александра52006

Геометрия

4,4(62 оценок)

ответ: 10; 4

Объяснение:

Дано:Δ МКР

∠К=90°;

КМ=12

КР=16

Найти R, r

представим такую картинку - у нас есть прямоугольник со сторонами 12 и 16, чему равна диагональ? Верно, по Пифагору она равна

√(12²+16²)=√400=20

а вокруг этого прямоугольника описана окружность. Чем является ее радиус? половиной диагонали, поскольку диагонали пересекаются и в точке пересечения делятся пополам. значит, если вытереть один треугольник, на который прямоугольник разбивает диагональ, то получим треугольник, описанный около окружности, с тем же радиусом. поэтому ответ на первую часть вопроса 20/2=10

что касаемо второй части, есть множество формул для нахождения радиуса вписанной окружности.

например; √((р-а)(р-b)(h-c)/р), р=Р/2=(20+12+16)/2=(10+8+6)=24

r=√(((24-20)*(24-12)(24-16)/24)=√(4*8*12/24)=√16=4

или так:(КМ+КР-РМ)/2=(12+16-20)/2=6+8-10=4

123456533

Геометрия

4,6(100 оценок)

60°

Объяснение:

Гипотенуза равна 24, а катет равен её половине т.е. 12.

Значит, катет лежит против угла 30°.

∠1=30°

∠2=90-30=60° т к сумма острых углов прямоугольного треугольника 90°

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.