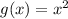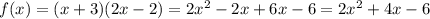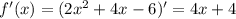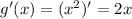Регистрация Спросить otvet5GPT
rahbfwBbdqbqdI
12.02.2020 06:07
Алгебра
Есть ответ 👍

Найди производную функции:у(х)= \frac{(x + 3)(2x - 2)}{ {x}^{2} } - 2 \cos2x

209
446
Посмотреть ответы 2

Ответы на вопрос:

shabdanova16
shabdanova16
4,8(20 оценок)

\boxed{y'(x) = \dfrac{4(3 - x)}{x^{3}} -4 \sin 2x}

Объяснение:

y(x) = \dfrac{(x + 3)(2x - 2)}{x^{2} } - 2 \cos 2x

Пусть:

f(x) = (x + 3)(2x - 2)

g(x) = {x^{2}

а)

f(x) = (x + 3)(2x - 2) = 2x^{2} - 2x + 6x - 6 = 2x^{2} + 4x - 6

б)

f'(x) = (2x^{2} + 4x - 6)' = 4x + 4

в)

g'(x) = (x^{2} )' = 2x

y'(x) = \bigg(\dfrac{(x + 3)(2x - 2)}{x^{2} } - 2 \cos 2x \bigg)' = \bigg ( \dfrac{(x + 3)(2x - 2)}{x^{2} } \bigg)' - \bigg(2 \cos 2x \bigg)'=

= \dfrac{4(3 - x)}{x^{3}} -4 \sin 2x

1)

\bigg ( \dfrac{(x + 3)(2x - 2)}{x^{2} } \bigg)' = \bigg ( \dfrac{f(x)}{g(x)} \bigg)' = \dfrac{f'(x)g(x) - f(x)g'(x)}{g^{2}(x)} =

= \dfrac{x^{2} (4x + 4) - 2x(2x^{2} + 4x - 6)}{(x^{2} )^{2}}= \dfrac{4x^{3} + 4x^{2} - (4x^{3} + 8x^{2} - 12x)}{x^{4}} =

= \dfrac{4x^{3} + 4x^{2} - 4x^{3} - 8x^{2} + 12x}{x^{4}} = \dfrac{12x - 4x^{2} }{x^{4}} = \dfrac{4x(3 - x)}{x \cdot x^{3}} = \dfrac{4(3 - x)}{x^{3}}

2)

\bigg(2 \cos 2x \bigg)'= 2 (\cos 2x)' = 2 \cdot (2x)' \cdot (-\sin 2x) = -4 \sin 2x


Найди производную функции:у(х)=
Найди производную функции:у(х)=
НяnKет
НяnKет
4,5(61 оценок)

(2√3-√5)²+2√60 = 12+5-2*2√3*√5+2√(4*15) = 12+5-4√15+4√15 = 17

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS