Математика: Найти точку минимума функции y = x^x

stars28082003

12.04.2021 02:52

Математика

Есть ответ 👍

Найти точку минимума функции y = x^x

115

342

Посмотреть ответы 3

Ответы на вопрос:

kirillanisimovp08nm9

Математика

4,4(25 оценок)

ответ: 1/е

Пошаговое объяснение:

ОДЗ х∈(0;+∞);

прологарифмируем обе части, они положительны, ㏑у=㏑(x^x);

㏑у=х㏑(x);

возьмем производную от обеих частей.

у'/y=㏑x+x/x

y'=(㏑x+1)*y;

y'=(㏑x+1)*(x^x); x^x≠0;

y'=0, если ㏑x+1=0, ㏑x=-1⇒х=е⁻¹; х=1/е

установим знаки, при переходе через критическую точку 1/е;

___01/е

- +

поэтому х=1/е- точка минимума.

kotlarovaira9

Математика

4,4(45 оценок)

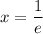ответ: $x=\dfrac{1}{e}$ .

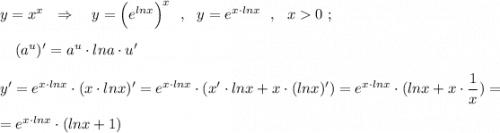
$y=x^{x}\ \ \Rightarrow \ \ \ y=\Big(e^{lnx}\Big)^{x}\ \ ,\ \ y=e^{x\cdot lnx}\ \ ,\ \ x 0\ ;{}\ \ \ (a^{u})'=a^{u}\cdot lna\cdot u'y'=e^{x\cdot lnx}\cdot (x\cdot lnx)'=e^{x\cdot lnx}\cdot (x'\cdot lnx+x\cdot (lnx)')=e^{x\cdot lnx}\cdot (lnx+x\cdot \dfrac{1}{x})==e^{x\cdot lnx}\cdot (lnx+1)$

Найдём стационарные (критические) точки.

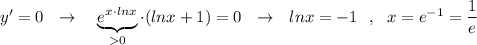
$y'=0\ \ \to \ \ \ \underbrace{e^{x\cdot lnx}}_{ 0}\cdot (lnx+1)=0\ \ \to \ \ lnx=-1\ \ ,\ \ x=e^{-1}=\dfrac{1}{e}$

Знаки y':

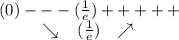
$(0)---(\frac{1}{e})\\{}\qquad \ \searrow \ \ \, (\frac{1}{e})\ \ \nearrow$

Так как производная меняет знак c минуса на плюс, то имеем точку минимума 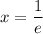$x=\dfrac{1}{e}$ .

azalia2003love

Математика

4,6(22 оценок)

5котлет умножаем на массу одной упаковки, и умножаем на 2 упаковки.. получаем 2400 грамм (в четырёх упаковках)

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Математика

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.