Ответы на вопрос:
Уравнение касательной:
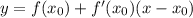
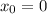
потому что касательная в точке (0;4).
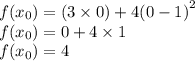
Найдем производную:
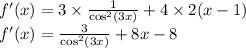
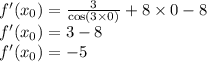
Подставим все в уравнение касательной
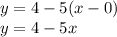
Уравнение касательной
y=4-5x
ответ: у=4-5х
Объяснение:
уравнение касательной у=f(x₀)+f'(x₀)*(x-x₀); здесь х₀=0;
f(x₀)=f(0)=tg0+4*(0-1)²=4 - точка (0;4) принадлежит графику функции f(x)=tg3x+4*(x-1)²;
f'(x)=(3/cos²(3x))+4*2*(x-1)*(x-1)'=(3/cos²(3x))+8*(x-1)*1=(3/cos²(3x))+8x-8;
f'(0)=(3/cos²(3*0))+8*0-8=3-8=-5;
уравнение касательной принимает такой вид: у=4-5*(х-0); у=4-5х;
Подставляем и решаем х+у=18.38+0.54=18.92., х-у=18.38-0.54=17.84. ху=18.38*0.54=9.93, х: у=18.38: 0.54=34
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Алгебра
-
сократите дроби 1) x^2-9/3x-9 2) x-3x/x+3 под корнем...
 bilingual06.05.2022 09:38
bilingual06.05.2022 09:38 -
Втаблице расстояния от солнца до четырёх планет солнечной системы. какая...
 AndreyMiix16.01.2023 02:36
AndreyMiix16.01.2023 02:36 -
реши систему уравнений способом сложения....
 innalemesh129.10.2022 09:52
innalemesh129.10.2022 09:52 -
Втреугольнике abc угол b=90градусов,угол acb=60градусов,cd-биссектрисса,найти...
 аня283511.03.2022 18:14
аня283511.03.2022 18:14 -
Разложить на множители ! (x-y)(x+y)+2(2x-y)+3 a в кубе-27+a в квадрате-3a...
 Алина111657723.03.2023 05:18
Алина111657723.03.2023 05:18 -
Решить два авто выехали одновременно из одного города в другой.скорость...
 Damirzic15.09.2021 20:05
Damirzic15.09.2021 20:05 -
Х²-6х+9 0 6) -4+4х-х²x04; 0 7) -х²-3х-2x05; 0 8) -2х²+х-1 0...
 чьзклу14.03.2020 10:47
чьзклу14.03.2020 10:47 -
Построить график и объяснить 1) y=1,5sin0,5x 2)y=sin(x-2pi/3)-2...
 Wolceme27.02.2023 00:01
Wolceme27.02.2023 00:01 -
Каким путем получается график функции y=sin|x|?...
 infernyc21.10.2020 19:00
infernyc21.10.2020 19:00 -
Докажите равенство: 4cos(п/6+a)*cos(п/6-a)=1-4sin^2a заранее...
 Дефектолог15.04.2023 14:48
Дефектолог15.04.2023 14:48

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

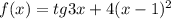 в точке (0; 4)
в точке (0; 4)