mysenjor

20.11.2021 22:22

Есть ответ 👍

Сторона основания правильной треугольной призмы равна 4 см, высота призмы равна 11√3 см. Вычисли объем и площадь поверхности призмы. 1)Объем призмы равен ⬜ см³.
2)Площадь поверхности призмы равна⬜ √3 см²

294

347

Посмотреть ответы 2

Ответы на вопрос:

ARKSHIM

Геометрия

4,4(30 оценок)

В основании призмы - правильный треугольник со стороной a = 4см, площадь правильного треугольника найдём по формуле Герона.

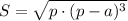
$S = \sqrt{p\cdot (p-a)^3}$

где p - полупериметр, то есть 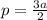$p = \frac{3a}{2}$

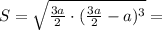
$S = \sqrt{\frac{3a}{2}\cdot (\frac{3a}{2} - a)^3} =$

$= \sqrt{\frac{3a}{2}\cdot (\frac{a}{2})^3} = \frac{a^2}{4}\cdot\sqrt{3}$

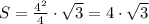$S = \frac{4^2}{4}\cdot\sqrt{3} = 4\cdot\sqrt{3}$ см²

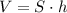
$V = S\cdot h$

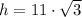$h = 11\cdot\sqrt{3}$ см

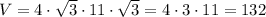$V = 4\cdot\sqrt{3}\cdot 11\cdot\sqrt{3} = 4\cdot 3\cdot 11 = 132$ см³

2) Площадь полной поверхности призмы

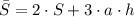
$\bar{S} = 2\cdot S + 3\cdot a\cdot h$

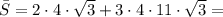
$\bar{S} = 2\cdot 4\cdot\sqrt{3} + 3\cdot 4\cdot 11\cdot\sqrt{3} =$

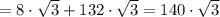$= 8\cdot\sqrt{3} + 132\cdot\sqrt{3} = 140\cdot\sqrt{3}$ см²

andrey451

Геометрия

4,5(36 оценок)

Объяснение:

Угол в 70° является вписанным и равен половине дуги ,на которую он опирается:

υАВ=2<BCA=2*70°=140°

υАВ=υВC=140°

υАC=360°-2υАВ=360°-280°=80°

<X является вписанным углом,который опирается на υАС,поэтому:

<X=1/2υАC=1/2*80°=40°

Задай свой вопрос

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.