zyxra4

19.05.2020 13:13

Математика

Есть ответ 👍

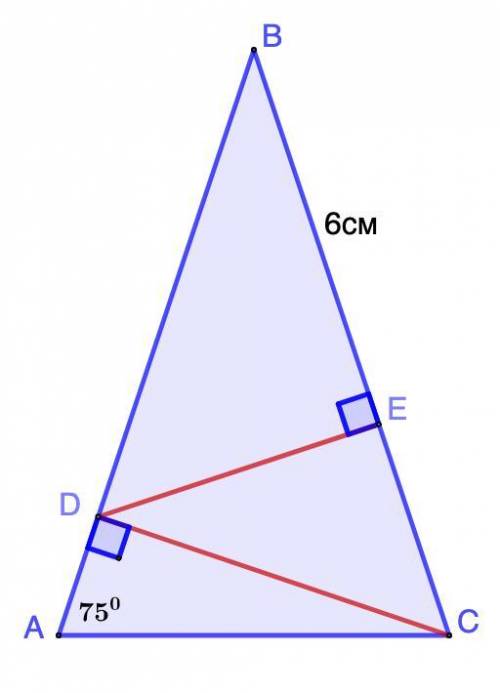
В равнобедренном треугольнике ABC с основанием AC угол A составляет 75 градусов, их угла С построен перпендикуляр СD к противолежащей стороне, точка D лежит на стороне AB. Из точки D построен перпендикуляр DE к стороне BC, точка Е лежит на стороне ВС. Известно, что отрезок ВЕ равен 6 см. Найди боковую сторону треугольника

191

327

Посмотреть ответы 2

Ответы на вопрос:

rabbit27

Математика

4,4(99 оценок)

Боковая сторона равно 8 см.

Пошаговое объяснение:

Требуется найти боковую сторону треугольника.

Дано: ΔАВС - равнобедренный.

∠А = 75°

CD ⊥ AB; DE ⊥ BC;

BE = 6 см

Найти: ВС

1. Рассмотрим ΔАВС - равнобедренный.

Углы при основании равнобедренного треугольника равны.

⇒ ∠А = ∠С = 75°

Сумма углов треугольника равна 180°.

⇒ ∠В = 180° - (∠А + ∠С) = 180° - 150° = 30°

2. Рассмотрим ΔBDE - прямоугольный.

∠В = 30°

Катет, лежащий против угла в 30°, равен половине гипотенузы.

⇒ DB = 2 DE

По теореме Пифагора:

DB² = DE² + BE²

или

(2DE)² = DE² + BE²

4DE² - DE² = 6²

3DE² = 36

DE² = 12

DE = 2√3 (см)

3. Рассмотрим Δ DВC - прямоугольный.

Сумма острых углов прямоугольного треугольника равна 90°.

⇒ ∠ВСD = 90° - ∠B = 90° - 30° = 60°

4. Рассмотрим Δ DEC - прямоугольный.

∠EDC = 90° - ∠ВСD = 90° - 60° = 30°

⇒ DC = 2 EC

По теореме Пифагора:

DC² = EC² + DE²

или

4EC² - EC² = 12

3EC² = 12 |:3

EC² = 4

EC = 2 (см)

5. ВС = ВЕ + ЕС = 6 + 2 = 8 (см)

Боковая сторона равно 8 см.

В равнобедренном треугольнике ABC с основанием AC угол A составляет 75 градусов, их угла С построен

Азрет2002

Математика

4,4(49 оценок)

ответ:

пошаговое объяснение:

вс и ад

можно провести высоту сн. тогда:

1) угол нсд=180 - 90-59=31

2) 121-31=90

следовательно вс и ад параллельны

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Математика

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.