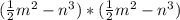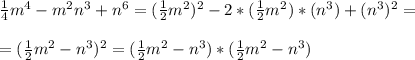Алгебра: 1/4м^4-м^2n^3+n^6 разложить на множители )

Andrey3355

15.04.2023 16:34

Алгебра

Есть ответ 👍

1/4м^4-м^2n^3+n^6 разложить на множители )

242

345

Посмотреть ответы 3

Ответы на вопрос:

mikhailsmirnov2

Алгебра

4,5(42 оценок)

=(1/2m^2)^2-(1/2m^2)*n^3*2+(n^3)^2=(m^2/2-n^3)^2
формула (a-b)^2=a^2-2ab+b^2

Nuruk04

Алгебра

4,6(72 оценок)

$(\frac{1}{2} m^2-n^3)*(\frac{1}{2} m^2-n^3)$

Объяснение:

$\frac{1}{4} m^4-m^{2} n^3+n^6=(\frac{1}{2} m^2)^2-2*(\frac{1}{2} m^2)*(n^3)+(n^3)^2==(\frac{1}{2} m^2-n^3)^2=(\frac{1}{2} m^2-n^3)*(\frac{1}{2} m^2-n^3)$

Использовалась формула (a-b)²=a²-2ab+b²

qwerty804

Алгебра

4,6(62 оценок)

Если в условии действительно h > |g + i|, то утверждение, очевидно, неверно: например, система 3x - y - z = 0 -x + 3y - z = 0 -x + 3y - z = 0 кроме решения (0, 0. 0) имеет решение (1, 1, 2). если в действительности i > |g + h|, g, h < 0, то утверждение становится верным: разделим первое уравнение на a, второе на e, третье на i и переобозначим получившиеся коэффициенты: x - ay - bz = 0 -cx + y - dz = 0 -ex - fy + z = 0 исходя из условия a, b, c, d, e, f > 0; a + b < 1, c + d < 1, e + f < 1. умножаем первое уравнение на c и складываем со вторым, умножаем на e и складываем с третьим: x - ay - bz = 0 (1 - ac) y - (d + bc) z = 0 -(f + ae) y + (1 - be) z = 0 так как 0 < a, b, c, e < 1, то 1 - ac, f + ae > 0. прибавим к третьему уравнению, домноженному на (1 - ac), второе, домноженное на (f + ae): x - ay - bz = 0 (1 - ac) y - (d + bc) z = 0 [(1 - ac)(1 - be) - (d + bc)(f + ae)] z = 0 рассматриваем коэффициент перед z в третьем уравнении: (1 - ac)(1 - be) - (d + bc)(f + ae) = 1 + abce - ac - be - df - bcf - ade - abce = 1 - (ac + be + df + bcf + ade) оценим выражение в скобках, учтя, что b < 1 - a, d < 1 - c, f < 1 - e: ac + be + df + bcf + ade < ac + (1 - a)e + (1 - c)(1 - e) + (1 - a)c(1 - e) + a(1 - c)e = 1. тогда коэффициент перед z положительный, на него можно разделить и получить, что z = 0. подставляем z = 0 во второе уравнение и получаем, что y = 0. подставляем y = z = 0 и получаем, что x = 0. x = y = z = 0, ура.

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Алгебра

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.