30.04.2020 05:05

Есть ответ 👍

498. Синус угла между образующей конуса, равной 100, и плоскостью основания равен 0,6. Найдите периметр соевого сечения конуса.
504.
Радиус основания конуса равен 2, а угол между образующей и плоскостью основания 60°. Найдите его объём.
P.s Дано, формула, решение.

276

374

Посмотреть ответы 2

Ответы на вопрос:

КИРИЛЛ9067

Геометрия

4,8(89 оценок)

1. Периметр соевого сечения конуса равен 360 ед.

2. Объем конуса 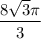$\displaystyle \frac{8\sqrt{3}\pi }{3}$ ед.³

Объяснение:

Требуется найти:

1. Периметр соевого сечения конуса.

2. Объем конуса.

498.

Дано: Конус.

АК = 100; sin∠АКО = 0,6.

Найти: Р (КАМ)

1. Рассмотрим ΔКАО - прямоугольный.

Синус угла - отношение противолежащего катета к гипотенузе.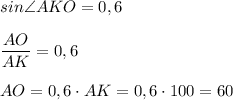

$\displaystyle sin\angle{AKO} = 0,6frac{AO}{AK}=0,6\\ \\AO = 0,6\cdot{AK} = 0,6\cdot100 = 60$

По теореме Пифагора:

КО² = АК² - АО²

КО² = 10000 - 3600 = 6400

КО = 80

⇒ КМ = 80 · 2 = 160

Р (КАМ) = АК + АМ + КМ = 100 + 100 + 160 = 360 (ед.)

504.

Дано: Конус;

r = СО = 2; ∠ВСО = 60°;

Найти: V конуса.

Объем конуса найдем по формуле:

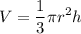$\displaystyle V=\frac{1}{3}\pi r^2h$ , где r - радиус основания, h - высота конуса.

1. Рассмотрим ΔСВО - прямоугольный.

Тангенс угла - отношение противолежащего катета к прилежащему.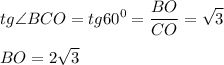

$\displaystyle tg\angle{BCO}=tg60^0=\frac{BO}{CO}=\sqrt{3} BO = 2\sqrt{3}$

2. Найдем объем:

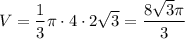$\displaystyle V=\frac{1}{3}\pi \cdot4\cdot2 \sqrt{3}=\frac{8\sqrt{3}\pi }{3}$ (ед.³)

498. Синус угла между образующей конуса, равной 100, и плоскостью основания равен 0,6. Найдите перим

daniil069531671

Геометрия

4,6(36 оценок)

180-(15+65)=180-80=100°

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.