Регистрация Спросить otvet5GPT
margaret1967m
22.10.2022 16:55
Геометрия
Есть ответ 👍

Докатите , что заданное уравнение является уравненнем сферы x² + y² + z² + 2x - 2y = 2 x ²+ y ²+ z² ' - 2x + 2z = 7

194
360
Посмотреть ответы 2

Ответы на вопрос:

yurasokolov232
yurasokolov232
4,5(37 оценок)

1)

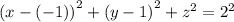
{(x - ( - 1))}^{2} + {(y - 1)}^{2} + {z}^{2} = {2}^{2}

2).

{(x - 1)}^{2} + {y}^{2} + {(z - ( - 1))}^{2} = {3}^{2}

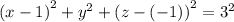
Объяснение:

1).

уравнение сферы с центром в точке А (х0;у0;z0) и радиусом r

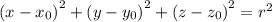
{(x - x_{0})}^{2} + {(y - y_{0}) }^{2} + {(z - z_{0}) }^{2} = {r}^{2}

выделим полные квадраты при переменных:

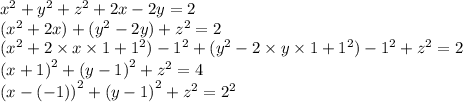
{x}^{2} + {y}^{2} + {z}^{2} + 2x - 2y = 2 \\ ( {x}^{2} + 2x) + ( {y}^{2} - 2y) + {z}^{2} = 2 \\ ( {x}^{2} + 2 \times x \times1 + {1}^{2}) - {1}^{2} + ( {y}^{2} - 2 \times y \times1 + {1}^{2}) - {1}^{2} + {z}^{2} = 2 \\ {(x + 1)}^{2} + {(y - 1)}^{2} + {z}^{2} = 4 \\ {(x - ( - 1))}^{2} + {(y - 1)}^{2} + {z}^{2} = {2}^{2}

- уравнение сферы с центром в точке А (-1;1;0) и радиусом r=2

2).

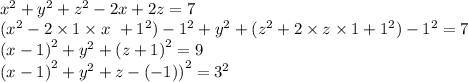
{x}^{2} + {y}^{2} + {z}^{2} - 2x + 2z = 7 \\ ( {x}^{2} - 2 \times 1 \times x \ + {1}^{2}) - {1}^{2} + {y}^{2} + ({z}^{2} + 2 \times z \times 1 + {1}^{2}) - {1}^{2} = 7 \\ {(x - 1)}^{2} + {y}^{2} + {(z + 1)}^{2} = 9 \\ {(x - 1)}^{2} + {y}^{2} + {z - ( - 1))}^{2} = {3}^{2}

- уравнение сферы с центром в точке А (1;0; -1) и радиусом r=3

soffia242004
soffia242004
4,8(47 оценок)

в условии не хватает длины стороны ав.

решим для ав = 4√2.

проведем высоту вн.

δавн: ∠анв = 90°, ∠ван = 45°, значит треугольник равнобедренный,

            вн = ан = х. по теореме пифагора

            x² + x² = (4√2)²

            2x² = 32

            x² = 16

            x = 4

вн = 4.

sabcd = (ad + bc)/2 · bh

sabcd = (13 + 7)/2 · 4 = 40 кв. ед.

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Геометрия

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS