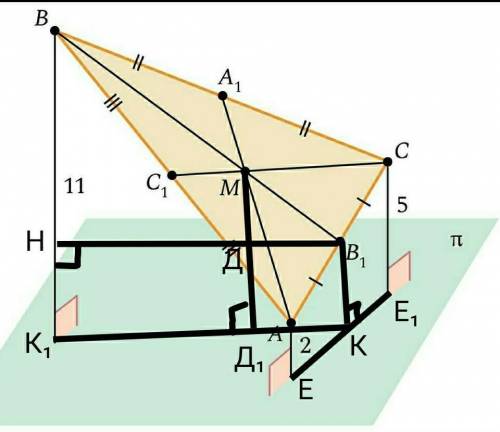
Треугольник ABC расположен в пространстве так, что расстояние от A до плоскости π равно 2, от B до плоскости π равно 11 и от C до плоскости π равно 5. Чему равно расстояние от точки пересечения медиан треугольника ABC до плоскости?

150

299

Посмотреть ответы 2

Ответы на вопрос:

ulyanan260801

Геометрия

4,8(30 оценок)

МД₁=6

Объяснение:

Искомым расстоянием от точки пересечения медиан М, до плоскости π является отрезок МД₁.

Обозначим высоты от стороны АС к плоскости π: В₁К, АЕ, СЕ₁. Соединим точки Е и Е₁. Получим трапецию ЕАСЕ₁. В₁К || АЕ || СЕ, так как они перпендикулярны плоскости π. По теореме Фалеса если параллельные прямые, пересекая стороны угла отсекают равные отрезки на одной его стороне, то они отсекают равные отрезки и на второй стороне угла, поэтому если АВ₁=В₁С, то ЕК=КЕ₁. → В₁К – средняя линия трапеции ЕАСЕ₁.

В₁К=(ЕА+Е₁С)÷2=(2+5)÷2=7÷2=3,5

Проведём перпендикуляры В₁Н и КК₁ к стороне ВК₁, получили трапецию В₁КК₁В.

В₁Н делит ВК₁, что К₁Н=В₁К=3,5, тогда ВН=11–3,5=7,5.

Рассмотрим ∆ВВ₁Н, он прямоугольный, ВН и В₁Н – катеты, ВВ₁ – гипотенуза. Медианы треугольника, пересекаясь, точкой пересечения делятся на отрезки в отношении 2 : 1, начиная от вершины треугольника, поэтому ВМ : МВ₁=2 : 1 и по теореме Фалеса ДН : В₁Д=2 : 1. МД || ВН, и МД отсекает от ∆ВВ₁Н подобный ему ∆МВ₁Д. Стороны ∆ВВ₁Н имеют 3 части (2+1=3), а стороны ∆МВ₁Д – одну часть. Пусть МД=х, запишем пропорцию:

МД : ВН=1 : 3

Произведение крайних членов пропорции равно произведению средних:

МД•3=ВН•1

3х=7,5•1

3х=7,5

х=7,5÷3

х=2,5

ДД₁=В₁К=НК₁=3,5

МД₁=МД+ДД₁=2,5+3,5=6

Треугольник ABC расположен в пространстве так, что расстояние от A до плоскости π равно 2, от B до п

assassin83arsoz7sda

Геометрия

4,8(54 оценок)

Объяснение:

эта таблица есть в инете загуглите по названию

UPD: Прикрепила)

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.