Регистрация Спросить otvet5GPT
MissEvaStar
31.01.2020 18:47
Алгебра
Есть ответ 👍

решить уравнение 6^cos2x>6^cos^2x+sinx.

186
251
Посмотреть ответы 3

Ответы на вопрос:

asjadorn
asjadorn
4,4(16 оценок)

6^cos2x>6^(cos^2x+sinx) ,6>1  знак неравенства не меняется

cos2x>cos²x+sinx

cos2x>cos²x+sinx

2cos²x-1>cos²x+sinx

2cos²x-1-cos²x-sinx>0

cos²x-1-sinx>0 |*(-1)

1-cos²x +sinx<0

sin²x+ sinx<0 <0 , sinx=t

t²+t<0  ,  t²+t=0 ⇒t=0 ,t=-1

+ + + (-1) - - - - (0)+ + + , -1<t<0

-1< sinx <0

-π/2+2πn<x<0+2πn,n∈Z

-π/2+2πn<x<2πn,n∈Z

красотка368
красотка368
4,8(73 оценок)

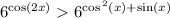
{6}^{ \cos(2x) } {6}^{ \cos {}^{2} (x) + \sin(x) }

Т.к основание слева и справа равны и больше 1, то показатели сносятся, а основание убирается, при этом знак неравенства сохраняется

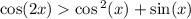
\cos(2x) \cos {}^{2} (x) + \sin(x)

Разложим cos(2x) по формуле и перенесем неизвестные влево

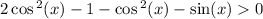
2 \cos {}^{2} (x) - 1 - \cos {}^{2} (x) - \sin(x ) 0

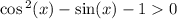
\cos {}^{2} ( x ) - \sin(x) - 1 0

Раскроем также cos²(x) по основному тригонометрическому тождеству

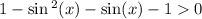
1 - \sin {}^{2} (x) - \sin(x) - 1 0

Умножим обе части неравенства на -1, при этом его знак поменяется

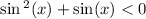
\sin {}^{2} (x) + \sin(x) < 0

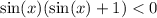
\sin(x) ( \sin(x) + 1) < 0

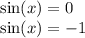
\sin(x) = 0 \\ \sin(x) = - 1

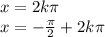
x = 2k\pi \\ x = - \frac{\pi}{2} + 2k\pi

Решим методом интервалов

(-pi/2)--{-}--(0)---{+}---(3pi/2)---{-}---(2pi)>

Требуется найти (<0), тогда в ответ пишем...

ответ: x€(3pi/2+2kpi;2kpi), k€Z

неха4уха
неха4уха
4,5(67 оценок)
(2cosx-3)/(4cosx+2)=4; ⇒(4cosx+2)≠0; ⇒ 2cosx-3=16cosx+8; ⇒ 14cosx=-11; cosx=-11/14; x=arccos(-11/14)+2kπ; k∈z; 3cosx-2< 4cosx+3/2; ⇒3cosx-4cosx< 2+3/2; ⇒-cosx< 7/2; ⇒ cosx> -7/2⇒cosx> -1

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS