1) Вычислить площадь фигуры, ограниченной заданными линиями 2) Найти объем тела, образованного вращением фигуры, ограниченной линиями
111
449
Ответы на вопрос:
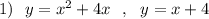
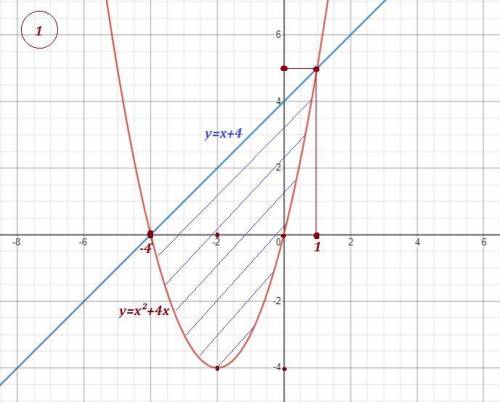
Найдём точки пересечения параболы и прямой.
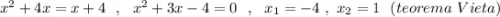
Площадь заданной области равна
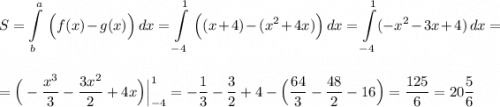
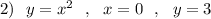
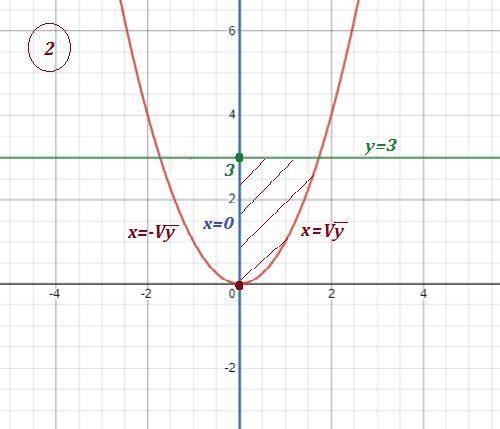
Объём тела, образованного вращением заданной фигуры
вокруг оси ОУ вычисляется по формуле 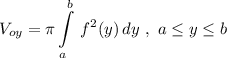
Здесь функция зависит от переменной "у" . Поэтому из уравнения параболы выразим "х" через "у" . Роль функции теперь играет "х" , а роль переменной - "у" .
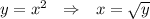 - уравнение правой ветви параболы. (Можно было взять и левую ветвь параболы
- уравнение правой ветви параболы. (Можно было взять и левую ветвь параболы 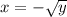 , всё равно при возведении в квадрат минус уйдёт) .
, всё равно при возведении в квадрат минус уйдёт) .
Из чертежа видно, что "у" изменяется от 0 до 3 .
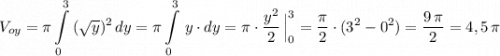
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Алгебра
-
Укажите решение системы неравенств...
 катя07210.04.2021 02:41
катя07210.04.2021 02:41 -
Решите Тема:Решения неравенств с одной переменной {х 3х 7 {х −6х ≥0 {х ≥...
 ianna9227p00tfn26.11.2021 17:51
ianna9227p00tfn26.11.2021 17:51 -
Найдите все значения параметра а, при каждом из которых, система имеет 3...
 yana102812.04.2022 17:49
yana102812.04.2022 17:49 -
надо решить до 3 часов ...
 Andreyvko120.03.2020 02:33
Andreyvko120.03.2020 02:33 -
Решите систему уравнений графическим...
 настя717628.11.2022 14:01
настя717628.11.2022 14:01 -
Розвяжіть рівняння: 1+6+11+...+x=342...
 slavabancov24.10.2022 03:06
slavabancov24.10.2022 03:06 -
задания очень надо кто как сможет Разложи на множители: 2t^4v^2+16tv^5....
 Катя38889105.06.2023 14:53
Катя38889105.06.2023 14:53 -
Обери пару натуральних чисел, яка задовольняє рівняння x+y=15 . Відповідь:...
 guarginia66622.02.2020 18:55
guarginia66622.02.2020 18:55 -
ДОМАШНЄ ЗАВДАННЯ №3 (1,2,3)...
 Ivan455412.04.2022 20:59
Ivan455412.04.2022 20:59 -
решить задачу: В кинотеатре m рядов по n мест в каждом и ещё k откидных...
 TTLoXoIMalchik11.12.2021 04:53
TTLoXoIMalchik11.12.2021 04:53

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.
