Геометрия: с задачей, очень важная контрольная,

андрей100500ый

18.10.2021 14:53

Геометрия

Есть ответ 👍

с задачей, очень важная контрольная,

114

407

Посмотреть ответы 2

Ответы на вопрос:

astatined

Геометрия

4,7(72 оценок)

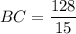
1. $BC=\dfrac{128}{15}$

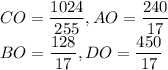
2. $CO=\dfrac{1024}{255},AO=\dfrac{240}{17}\\BO=\dfrac{128}{17},DO=\dfrac{450}{17}$

Объяснение:

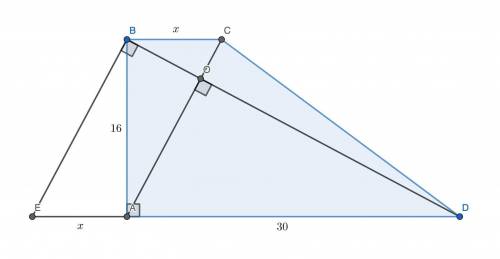
1. Отложим от точки B отрезок BE такой, что он лежит на прямой, параллельной AC, а точка E лежит на прямой AD (то есть выполним параллельный перенос отрезка AC на вектор CB). Поскольку EA || BC как прямые, содержащие основания трапеции, а AC || BE по построению, то AEBC — параллелограмм, откуда BC = EA. Поскольку углы ∠AOD и ∠EBD соответственные при параллельных прямых AC и EB, то они равны, а значит, EB ⊥ BD. Но BA ⊥ ED по условию, значит, в прямоугольном ΔEBD BA — высота, опущенная из прямого угла. Тогда 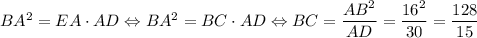$BA^2=EA\cdot AD\Leftrightarrow BA^2=BC\cdot AD\Leftrightarrow BC=\dfrac{AB^2}{AD}=\dfrac{16^2}{30}=\dfrac{128}{15}$ .

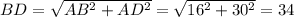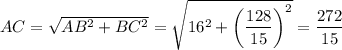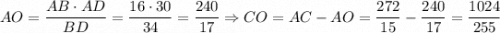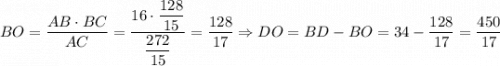2. В прямоугольном ΔABD $BD=\sqrt{AB^2+AD^2}=\sqrt{16^2+30^2}=34$ . В прямоугольном ΔABC $AC=\sqrt{AB^2+BC^2}=\sqrt{16^2+\left(\dfrac{128}{15}\right)^2}=\dfrac{272}{15}$ . AO — высота, опущенная из прямого угла, $AO=\dfrac{AB\cdot AD}{BD}=\dfrac{16\cdot 30}{34}=\dfrac{240}{17}\Rightarrow CO=AC-AO=\dfrac{272}{15}-\dfrac{240}{17}=\dfrac{1024}{255}$ . Аналогично $BO=\dfrac{AB\cdot BC}{AC}=\dfrac{16\cdot\dfrac{128}{15}}{\dfrac{272}{15}}=\dfrac{128}{17}\Rightarrow DO=BD-BO=34-\dfrac{128}{17}=\dfrac{450}{17}$ .

BashProcker

Геометрия

4,6(21 оценок)

Ребро С1B1 не является высотой пирамид С1B1BA1 и BC1A1A , но высота , проведенная из С1 у них общая ( пояснение к решению)

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.