Регистрация Спросить otvet5GPT
Варвараминнннн
09.08.2022 04:17
Алгебра
Есть ответ 👍

Доказать неравенство за

291
377
Посмотреть ответы 2

Ответы на вопрос:

tatianani
tatianani
4,4(99 оценок)

Объяснение:

\displaystyle\sqrt[3]{\frac{x^3+y^3}{2} } \geq \frac{x+y}{2} (x0,y0)

обе части положительны, возведем в куб

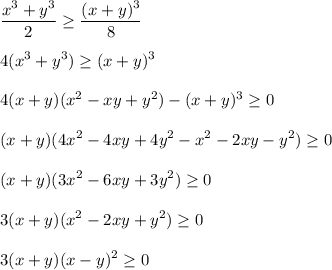
\displaystyle\frac{x^3+y^3}{2} \geq \frac{(x+y)^3}{8} 4(x^3+y^3)\geq (x+y)^34(x+y)(x^2-xy+y^2)-(x+y)^3\geq 0(x+y)(4x^2-4xy+4y^2-x^2-2xy-y^2)\geq 0(x+y)(3x^2-6xy+3y^2)\geq 03(x+y)(x^2-2xy+y^2)\geq 03(x+y)(x-y)^2\geq 0

данное неравенство верно:

второй множитель х+у больше нуля,

поскольку х>0,y>0

(x-y)²≥0  квадрат любой величины ≥0

исходное неравенство тоже верно

доказано

senazubik63kfkd
senazubik63kfkd
4,4(8 оценок)

Смотри фото

---------------------

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS