Xn=3n/n+1 Найти:
1)Член x1; x4;x9;x99;x999.
2)Определить вырастает или убывает последовательность.
3) Определить ограниченность.

193

337

Посмотреть ответы 2

Ответы на вопрос:

rasukka

Математика

4,6(95 оценок)

1) x₁ = 1,5; x₄ = 2,4; x₉ = 2,7; x₉₉ = 2,97; x₉₉₉ = 2,997;

2) строго возрастает;

3) ограничена.

Пошаговое объяснение:

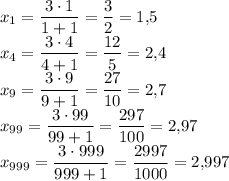
1) $x_1=\dfrac{3\cdot 1}{1+1}=\dfrac{3}{2}=1{,}5\\x_4=\dfrac{3\cdot 4}{4+1}=\dfrac{12}{5}=2{,}4\\x_9=\dfrac{3\cdot 9}{9+1}=\dfrac{27}{10}=2{,}7\\x_{99}=\dfrac{3\cdot 99}{99+1}=\dfrac{297}{100}=2{,}97\\x_{999}=\dfrac{3\cdot 999}{999+1}=\dfrac{2997}{1000}=2{,}997$

2) Оценим разность 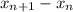$x_{n+1}-x_n$ :

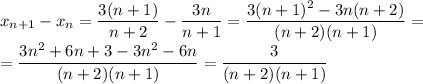
$x_{n+1}-x_n=\dfrac{3(n+1)}{n+2}-\dfrac{3n}{n+1}=\dfrac{3(n+1)^2-3n(n+2)}{(n+2)(n+1)}=\\=\dfrac{3n^2+6n+3-3n^2-6n}{(n+2)(n+1)}=\dfrac{3}{(n+2)(n+1)}$

Поскольку n ≥ 1 (как натуральное число), n + 2 > 0, n + 1 > 0. Тогда 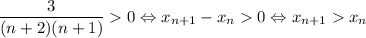$\dfrac{3}{(n+2)(n+1)}0\Leftrightarrow x_{n+1}-x_n0\Leftrightarrow x_{n+1}x_n$ — каждый следующий член строго больше предыдущего, значит, последовательность строго возрастает.

3) Поскольку последовательность строго возрастает, она ограничена снизу первым членом. Проверим ограниченность сверху:

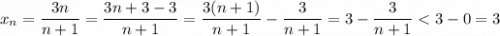
$x_n=\dfrac{3n}{n+1}=\dfrac{3n+3-3}{n+1}=\dfrac{3(n+1)}{n+1}-\dfrac{3}{n+1}=3-\dfrac{3}{n+1}$

Последовательность ограничена сверху. Поскольку она ограничена и сверху, и снизу, то она ограниченная.

llvoronall

Математика

4,4(77 оценок)

за 1 час и 40 минут (1⅔) первый поезд прошёл 63*1⅔=105 км. между ними осталось 473-105=368 км. скорость сближения 63+52=115. они встретятся через 368/115=3,2 переводим в часы ⇒ 3 часа и 12 минут.

ответ: 3 часа и 12 минут

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Математика

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.