Регистрация Спросить otvet5GPT
karinaeruslanov
13.03.2023 10:32
Математика
Есть ответ 👍

Сррчно оаоаоаооаоаоао

216
440
Посмотреть ответы 3

Ответы на вопрос:

SLI2000a
SLI2000a
4,5(65 оценок)

18,7 т.к -в модуле уходят и можно просто сложить все числа и получится 18,7

Amalya15
Amalya15
4,6(62 оценок)

Модуль всегда положительный.

|1.8|+|-2.3|+|4.7|+|-5.8|+|-4.1|

=> 1.8+2.3+4.7+5.8+4.1=18.7

anton4rf4
anton4rf4
4,4(51 оценок)

-1

Пошаговое объяснение:

Заметим, что если x является решением уравнения, то и -x также является решением уравнения (действительно, возведение в квадрат, в четвёртую степень и взятие косинуса "убивает" минус). Значит, необходимое условие единственности решения: x = -x ⇒ x = 0 (условие не достаточное, так как помимо 0 могут быть и другие решения, поэтому каждое значение параметра необходимо будет проверить).

Подставим x = 0 в уравнение:

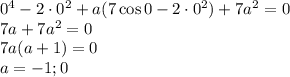
0^4-2\cdot 0^2+a(7\cos{0}-2\cdot 0^2)+7a^2=0\\7a+7a^2=0\\7a(a+1)=0\\a=-1;0

Если a = 0, то уравнение имеет вид:

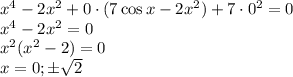
x^4-2x^2+0\cdot (7\cos{x}-2x^2)+7\cdot 0^2=0\\x^4-2x^2=0\\x^2(x^2-2)=0\\x=0;\pm\sqrt{2}

Три решения, a = 0 не подходит.

Если a = -1:

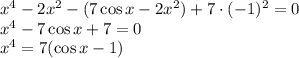
x^4-2x^2-(7\cos{x}-2x^2)+7\cdot(-1)^2=0\\x^4-7\cos{x}+7=0\\x^4=7(\cos{x}-1)

Заметим, что 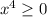x^4\geq 0, а \cos{x}-1\leq 0, то есть левая часть не меньше нуля, а правая — не больше нуля. Равенство достигается, когда обе части равны нулю:

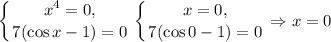\displaystyle\left \{ {{x^4=0,} \atop {7(\cos{x}-1)=0}} \right. \left \{ {{x=0,} \atop {7(\cos{0}-1)=0}} \right. \Rightarrow x=0— единственное решение. a = -1 подходит.

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Математика

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS