Ответы на вопрос:
Найдём длину каждой стороны этого треугольника.
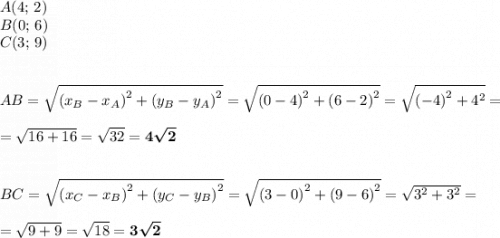
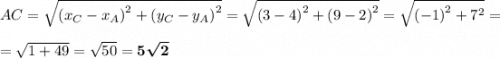
Чтобы определить вид треугольника, нам надо определить вид наибольшего угла этого треугольника. Наибольший угол в треугольнике всегда лежит напротив его наибольшей стороны, поэтому расписываем теорему косинусов для стороны 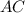 :
:
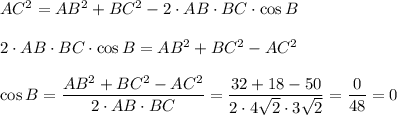
Если косинус  равен 0, значит, этот угол прямой. Отсюда делаем вывод, что треугольник с заданными точками является прямоугольным.
равен 0, значит, этот угол прямой. Отсюда делаем вывод, что треугольник с заданными точками является прямоугольным.
ответ: 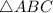 - прямоугольный.
- прямоугольный.
если диаметр равен двум радиусам, а радиусы всегда равны между собой то получается что диаметр делится центром окружности на 2 равных отрезка.
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Математика
-
Народ решить : магазин получил 560кг овощей. в первый день продали пять...
 kopiplay29.09.2022 08:28
kopiplay29.09.2022 08:28 -
Найди площадь квадрата со стороной 5 см среди чисел: а.20см в.29см2...
 родтчса02.02.2023 03:02
родтчса02.02.2023 03:02 -
Как решить такую . площадь основания прямоугольной призмы 18 см2 а высота...
 leiylacan109.01.2023 18:05
leiylacan109.01.2023 18:05 -
Укажи столбик уравнения которого имеют один и тот же корень...
 я00124.12.2021 14:29
я00124.12.2021 14:29 -
В280 мешках на 2250 кг риса больше чем 230 мешках. сколько риса в каждом...
 marija0102126.02.2022 17:35
marija0102126.02.2022 17:35 -
Один из четырёх объектов «лишний»? какой именно и почему? вернер фон...
 Angelochek0230.12.2022 23:24
Angelochek0230.12.2022 23:24 -
Найди значение выражений: (6м--26дм)...
 андрей209630.05.2021 18:43
андрей209630.05.2021 18:43 -
Уумножить на 62 минус 5802 равно 3870 ответ уравнений...
 nurgisaabish1234528.09.2022 10:32
nurgisaabish1234528.09.2022 10:32 -
Хватит ли 900 г глины для изготовления 4 кружек если для одной кружки...
 Lumenarix14.06.2020 15:02
Lumenarix14.06.2020 15:02 -
Кто нибудь объясните как расписать 615: 3=205 нужно расписать а столбик....
 nikitamarar217718.06.2023 09:54
nikitamarar217718.06.2023 09:54

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.
