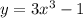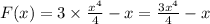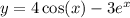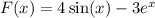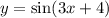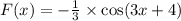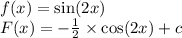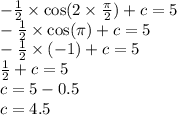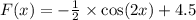Регистрация Спросить otvet5GPT
anna1870
11.03.2020 08:42
Алгебра
Есть ответ 👍

Знайдіть область визначення функції

, очень надо(((

229
234
Посмотреть ответы 2

Ответы на вопрос:

Amid05
Amid05
4,8(37 оценок)

Область определения функции

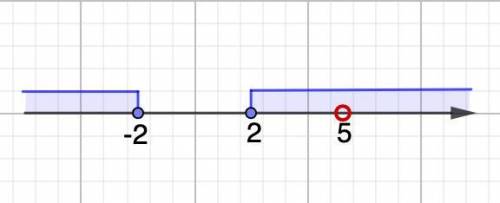
D(y) = (-∞; -2] ∪ [2; 5) ∪ (5; +∞)

Объяснение:

Требуется найти область определения функции.

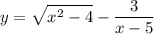
\displaystyle y= \sqrt{x^2-4}-\frac{3}{x-5}

Область определения функции — это множество всех значений аргумента (переменной x)

Используем следующие правила:

Подкоренное выражение неотрицательно.На ноль делить нельзя!

Получим  систему:

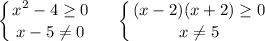
\displaystyle \left \{ {{x^2 - 4\geq 0} \atop {x-5\neq 0}} \right. \;\;\;\;\;\left \{ {{(x-2)(x+2)\geq 0} \atop {x\neq 5}} \right. \;\;\;\;\;

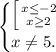
\displaystyle \\ \begin{equation*} \begin{cases} \left [{x\leq -2} \atop {x\geq 2} \right. \\ x \ne 5. \end{cases}\end{equation*}

Отметим решение на числовой оси.(см.рис)

Получим ответ:

D(y) = (-∞; -2] ∪ [2; 5) ∪ (5; +∞)


Знайдіть область визначення функції , очень надо(((
katyaaaasd
katyaaaasd
4,4(95 оценок)

а)

y = 3 {x}^{3} - 1

F(x) = 3 \times \frac{ {x}^{4} }{4} - x = \frac{3 {x}^{4} }{4} - x

б)

y = 4 \cos(x) - 3 {e}^{x}

F(x) = 4 \sin(x) - 3 {e}^{x}

в)

y = \sin(3x + 4)

F(x) = - \frac{1}{3} \times \cos(3x + 4)

2.

f(x) = \sin(2x) \\ F(x) = - \frac{1}{2} \times \cos(2x) + c

M (π/2;5)

- \frac{1}{2} \times \cos(2 \times \frac{\pi}{2} ) + c = 5 \\ - \frac{1}{2} \times \cos(\pi) + c = 5 \\ - \frac{1}{2} \times ( - 1) + c = 5 \\ \frac{1}{2} + c = 5 \\ c = 5 - 0.5 \\ c = 4.5

F(x) = - \frac{1}{2} \times \cos(2x) + 4.5

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS