26.05.2021 22:27

Есть ответ 👍

Сколько существует целых значений a, при которых неравенство дальше во вложении

201

368

Посмотреть ответы 2

Ответы на вопрос:

машунька0811

Математика

4,4(17 оценок)

0; 1; 2

Пошаговое объяснение:

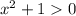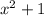Так как x^2 + 1 0 для любого , то можно умножить все части неравенства на x^2 + 1 , при этом сохранив знаки.

Получим

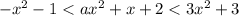
-x^2 - 1 < ax^2 + x + 2 < 3x^2 + 3

Рассмотрим первое неравенство

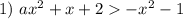
$1) \ ax^2 + x + 2 -x^2 - 1$

(a + 1)x^2 + x + 3 0

Данному неравенству соответствует парабола

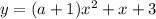
y = (a + 1)x^2 + x + 3

Для того, чтобы для всех значения параболы были положительны, необходимо и достаточно выполнение двух условий:

а) Ветви параболы должны быть направлены вверх, то есть

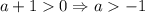
$a + 1 0 \Rightarrow a -1$

б) Парабола не должна пересекать ось 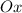(у неё не должно быть корней), то есть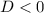 D < 0

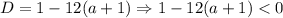
$D = 1 - 12(a + 1) \Rightarrow 1 - 12(a + 1) < 0$

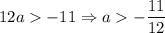
$12a -11 \Rightarrow a -\dfrac{11}{12}$

Из приведённых условий

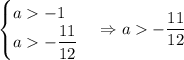
$\begin{cases} a -1 \\a -\dfrac{11}{12}\end{cases} \Rightarrow a -\dfrac{11}{12}$

Рассмотрим второе неравенство

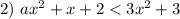
$2) \ ax^2 + x + 2 < 3x^2 + 3$

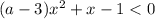
(a - 3)x^2 + x - 1 < 0

Данному неравенству соответствует парабола

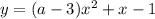
y = (a - 3)x^2 + x - 1

Для того, чтобы для всех значения параболы были отрицательны, необходимо и достаточно выполнение двух условий:

а) Ветви параболы должны быть направлены вниз, то есть

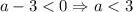
$a - 3 < 0 \Rightarrow a < 3$

б) Парабола не должна пересекать ось (у неё не должно быть корней), то есть D < 0

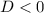
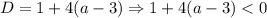
$D = 1 + 4(a - 3) \Rightarrow 1 + 4(a - 3) < 0$

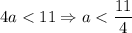
$4a < 11 \Rightarrow a < \dfrac{11}{4}$

Из приведённых условий

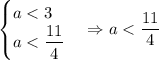
$\begin{cases} a < 3 \\a < \dfrac{11}{4}\end{cases} \Rightarrow a < \dfrac{11}{4}$

В итоге для двойного неравенства

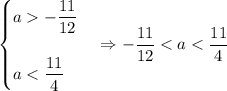
$\begin{cases} a -\dfrac{11}{12} \\ \\a < \dfrac{11}{4}\end{cases} \Rightarrow -\dfrac{11}{12} < a < \dfrac{11}{4}$

В данном промежутке лежат следующие целые значения :

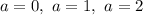
$a = 0, \ a = 1, \ a = 2$

Сколько существует целых значений a, при которых неравенство дальше во вложении

kurzinovaa

Математика

4,6(12 оценок)

Пошаговое объяснение:

1) (0.5x+1.5x+x)÷3=1.2

3x=1.2×3

3x=3.6

x=3.6÷3

x=1.2

2) 0.5x=0.5×1.2=0.6

3) 1.5x=1.5×1.2=1.8

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Математика

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.