Регистрация Спросить otvet5GPT
ponchikelo
19.06.2022 10:57
Геометрия
Есть ответ 👍

Дана окружность с центром в точке O (-2; 3) и диаметром 8, и y = −2х + 3. а) Запишите уравнение окружности.
б) Найдите точки пересечения окружности и прямой.
в) Найдите точки пересечения прямой с осями координат.
г) Найдите точки пересечения окружности с осями координат.

200
353
Посмотреть ответы 2

Ответы на вопрос:

kabulbekova01
kabulbekova01
4,4(20 оценок)

а) Найдем уравнение окружности:

(x-a)²+ (y-b)²=r² (а и b — координаты центра окружности, r – радиус)

r=d/2=8/2=4

Уравнение нашей окружности:

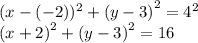
(x - ( - 2))^{2} + {(y - 3)}^{2} = {4}^{2} \\ {(x + 2)}^{2} + {(y - 3)}^{2} = 16

б) Чтобы найти точку пересечения надо подставить уравнение прямой на уравнение окружности вмести y

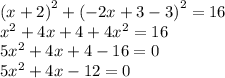
{(x + 2)}^{2} + {( - 2x + 3 - 3)}^{2} = 16 \\ {x}^{2} + 4x + 4 + 4 {x}^{2} = 16 \\ 5 {x}^{2} + 4x + 4 - 16 = 0 \\ 5 {x}^{2} + 4x - 12 = 0

a=5, b=4, c=-12

Найдем по дискриминанту

D=b²-4ac

D=4²-4×5×(-12)=16+240=256

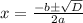
x = \frac{ - b \pm \sqrt{D} }{2a}

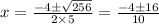
x = \frac{ - 4 \pm \sqrt{256} }{2 \times 5} = \frac{ - 4 \pm 16}{10}

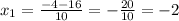
x_{1} = \frac{ - 4 - 16}{10} = - \frac{20}{10} = - 2

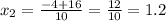
x_{2} = \frac{ - 4 + 16}{10} = \frac{12}{10} = 1.2

Подставим x в уравнение прямой

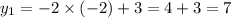
y_{1} = - 2 \times ( - 2) +3 = 4 + 3 = 7

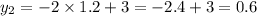
y_{2} = - 2 \times 1.2 + 3 = - 2.4 + 3 = 0.6

Точки пересечения окружности и прямой

Точки пересечения окружности и прямой(-2 ; 7) и (1,2 ; 0,6)

в) чтобы найти пересечение с осями координат надо приравнять x и y нулю по очереди. Если найти с осью Oy, то надо приравнять x к нулю. А если найти пересечения с осью Ox, то надо приравнять y к нулю.

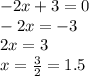
- 2x + 3 = 0 \\ - 2x = - 3 \\ 2x = 3 \\x = \frac{3}{2} = 1.5

Прямая пересекает ось Ox в точке (1,5 ; 0)

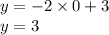
y = - 2 \times 0 + 3 \\ y = 3

Прямая пересекает ось Oy в точке (0 ; 3)

г)

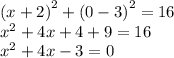
{(x + 2)}^{2} + {(0 - 3)}^{2} = 16 \\ {x}^{2} + 4x + 4 + 9 = 16 \\ {x}^{2} + 4x - 3 = 0

D=16+12=28

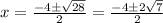
x = \frac{ - 4 \pm \sqrt{28}}{2} = \frac{ - 4 \pm 2 \sqrt{7} }{2}

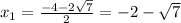
x_{1} = \frac{ - 4 - 2 \sqrt{7} }{2} = - 2 - \sqrt{7}

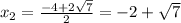
x_{2} = \frac{ - 4 + 2 \sqrt{7} }{2} = - 2 + \sqrt{7}

Окружность пересекает ось Ox в точках (-2-√7 ; 0) и (-2+√7 ; 0)

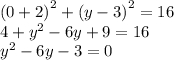
{(0 + 2)}^{2} + {(y - 3)}^{2} = 16 \\ 4 + {y}^{2} - 6y + 9 = 16 \\ {y}^{2} - 6y - 3 = 0

D=36+12=48

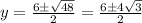
y = \frac{6 \pm \sqrt{48} }{2} = \frac{6 \pm 4 \sqrt{3} }{2}

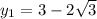
y_{1} = 3 - 2 \sqrt{3}

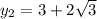
y_{2} = 3 + 2 \sqrt{3}

Окружность пересекает ось Oy в точках (0 ; 3-2√3) и (0 ; 3+2√3)

ЮлияБогинская
ЮлияБогинская
4,5(84 оценок)

всё правельно).

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Геометрия

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS