X²-92=y²+2y Найдите количество пар целых чисел

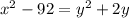
Заметим, что если в правой части добавить 1, то получим формулу квадрата суммы. Тогда, добавим 1 и в левой и в правой части:

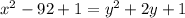
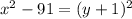
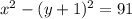
Применим формулу разности квадратов:

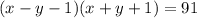
Заметим, что если 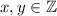, то обе скобки, записанные в левой части, дают целые числа.

Разложим число 91 на простые множители:

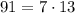
Тогда, число 91 можно получить путем умножения либо чисел 7 и 13, либо чисел 1 и 91. Нужно учесть, что эти числа могут умножаться в разных порядках, а также то, что оба множителя могут поменять знак на противоположный.

Таким образом есть 8 упорядоченных пар целых чисел, в произведении дающих 91:

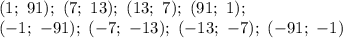
Но данные пары целых чисел соответствуют скобкам в произведении 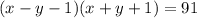. Необходимо проверить, будут ли сами числа и 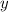в каждом из этих случаев целыми. Можно составить и решить 8 систем, но вместо этого мы составим одну систему в общем виде, решим ее опять же в общем виде и проанализируем результаты.

Рассмотрим систему:

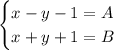
Пусть 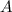и 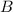- целые числа. Решим систему методом сложения. Сложив уравнения, получим:

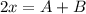
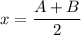
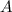Заметим, что является целым числом, когда и 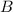имеют одинаковую четность.

Из второго уравнения выразим :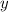

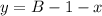
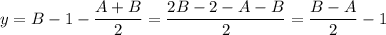
Аналогично, 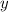является целым числом, когда 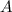и 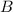имеют одинаковую четность.

Но все числа в наших парах:

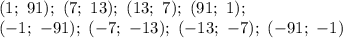
имеют одинаковую четность. Значит, все 8 систем дадут по одному решению в целых числах. Таким образом, исходное уравнение имеет 8 решений в целых числах.

ответ: 8

Очевидно, что искать надо среди чисел, которые на 1 меньше полных квадратов, т.к. дробная часть корня этих чисел будет максимально приближена к 0,99. т.к.  √n=a, получаем неравенство √n≥a,99, √n≥a+0,99 обозначим    (1), одновременно с этим должно выполняться неравенство  √n< a+1 обозначим (2) т.к. число n   на 1  меньше полного квадрата, то  √(n+1)=a+1 обозначим (3), возведем обе части (3) в квадрат, получим n+1=a²+2a+1, n=a²+2a (4), возведем   обе части (2)в квадрат, получим n< a²+2a+1, подставим n из (4), получим a²+2a< a²+2a+1, 0< 1, что всегда выполняется, значит, при данных условиях неравенство (2) всегда выполняется.тогда, получаем, что нужно решить систему    √n≥a+0,99  (1),  √(n+1)=a+1  (3), где n,a  - натуральные числа, и надо найти наименьшие.мы уже получили равенство (4) из равенства (3). возведем в квадрат обе части (1) и подставим n из (4): n≥(a+0,99)², a²+2a≥a²+1,98a+0,9801, 0,02a≥0,9801, a≥0,9801/0,02, a≥49,005 ближайшее целое a=50, тогда  √(n+1)=51, n+1=2601, n=2600 ответ: наименьшее  n=2600