Регистрация Спросить otvet5GPT
Happy0cake
26.07.2022 22:22
Алгебра
Есть ответ 👍

Решите уравнения, используя умножение на сопряженное уравнение: √(3х²-7х+3)-√(х²-2)=√(3х²-5х-1)-√(х²-3х+4)

214
320
Посмотреть ответы 2

Ответы на вопрос:

julija74
julija74
4,4(61 оценок)

Объяснение:

Решите уравнения, используя умножение

на сопряженное уравнение:

√(3х²-7х+3)-√(х²-2)=√(3х²-5х-1)-√(х²-3х+4)

преобразуем

√(3х²-7х+3)-√(3х²-5х-1)=√(х²-2)-√(х²-3х+4)

Применяя метод домножения на сопряжённое выражение, преобразуем левую и правую части уравнения:

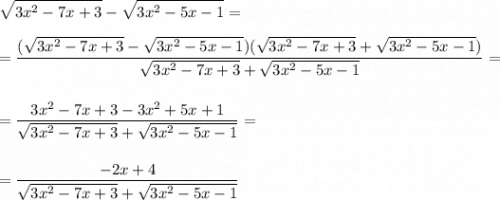
\displaystyle\\\sqrt{3x^2-7x+3} -\sqrt{3x^2-5x-1} ==\frac{(\sqrt{3x^2-7x+3} -\sqrt{3x^2-5x-1})(\sqrt{3x^2-7x+3} +\sqrt{3x^2-5x-1})}{\sqrt{3x^2-7x+3} +\sqrt{3x^2-5x-1}} ==\frac{3x^2-7x+3-3x^2+5x+1}{\sqrt{3x^2-7x+3} +\sqrt{3x^2-5x-1}} ==\frac{-2x+4}{\sqrt{3x^2-7x+3} +\sqrt{3x^2-5x-1}}

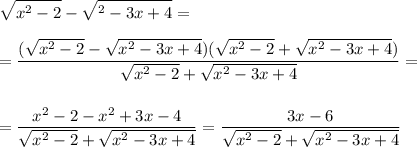
\displaystyle\\\sqrt{x^2-2} -\sqrt{^2-3x+4}==\frac{(\sqrt{x^2-2} -\sqrt{x^2-3x+4})(\sqrt{x^2-2} +\sqrt{x^2-3x+4})}{\sqrt{x^2-2} +\sqrt{x^2-3x+4}} ==\frac{x^2-2-x^2+3x-4}{\sqrt{x^2-2} +\sqrt{x^2-3x+4}} = \frac{3x-6}{\sqrt{x^2-2} +\sqrt{x^2-3x+4}}

уравнение принимает вид

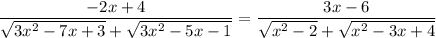
\displaystyle\frac{-2x+4}{\sqrt{3x^2-7x+3} +\sqrt{3x^2-5x-1}}=\frac{3x-6}{\sqrt{x^2-2} +\sqrt{x^2-3x+4}}

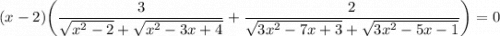
\displaystyle\\(x-2)\bigg(\frac{3}{\sqrt{x^2-2}+\sqrt{x^2-3x+4} } +\frac{2}{\sqrt{3x^2-7x+3} +\sqrt{3x^2-5x-1} } \bigg)=0

выражение во вторых скобках строго положительно

x-2=0

x=2

подстановкой в исходное уравнение убеждаемся, что х=2

является корнем данного уравнения

ответ: x=2

DaNa1517
DaNa1517
4,6(60 оценок)
Ого! а тут те чертить надо никак тут не написать мне

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS