Регистрация Спросить otvet5GPT
Helpmeplz123
20.04.2023 21:07
Алгебра
Есть ответ 👍

Решите систему уравнений xy^2=8 4x-y^2=0

129
257
Посмотреть ответы 2

Ответы на вопрос:

Deva0revolution
Deva0revolution
4,8(17 оценок)

Объяснение:

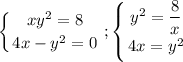
\displaystyle\\\left \{ {{xy^2=8} \atop {4x-y^2=0}} \right. ;\left \{ {{y^2=\dfrac{8}{x} } \atop {4x=y^2}} \right.

из первого уравнения следует, что х>0

подставим значение y² во второе уравнение и решим его

4x=\dfrac{8}{x} ;x=\dfrac{2}{x} ;x^2=2;x=\sqrt{2} y^2=\dfrac{8}{\sqrt{2} } =\dfrac{8\sqrt{2} }{2}=4\sqrt{2} y=\pm2\sqrt[4]{2} Otvet:(\sqrt{2} ;-2\sqrt[4]{2} );~~(\sqrt{2} ;2\sqrt[4]{2} )

amwarawka
amwarawka
4,4(96 оценок)

1) выделяем полные квадраты:

для y:   (y²+2*7y + 72) -1*72 = (y+7)²-49

преобразуем исходное уравнение:

(y+7)² = 6x - 0

получили уравнение параболы:

(y - y0)² = 2p(x - x0)

(y+7)² = 2*3(x - 0)

ветви параболы направлены вправо, вершина расположена в точке (x0, y0), т.е. в точке (0; -7)

параметр p = -3.

координаты фокуса:   f(-p/2; yo) = (-1,5; -7).

уравнение директрисы: x = x0 - p/2

x = 0 - 3/2 = -3/2.

2) выделяем полные квадраты:

для x:   (x²-2*1x + 1) -1 = (x-1)²-1

для y:   -4(y²+2*3y + 3²2) +4*3² = -4(y+3)²+36

в итоге получаем:

(x-1)²-4(y+3)² = -68

разделим все выражение на -68

(-1/68)(x - 1)² + (1/17)(y + 3)² = 1.

параметры кривой.

данное уравнение определяет гиперболу с центром в точке:

c(1; -3)

и полуосями:   a = 2√17, b =√17.

найдем координаты ее фокусов: f1(-c; 0) и f2(c; 0), где c - половина расстояния между фокусами

определим параметр c: c² = a² + b² = 68 + 17 = 85

c = √85.

тогда эксцентриситет будет равен:   e = c/a = √85/2√17.

асимптотами гиперболы будут прямые:   y + 3 = (1/2)(x - 1) и

y + 3 = (-1/2)(x - 1).

директрисами гиперболы будут прямые:   +-е/а = +-(√68/√85).

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS