С объяснением . Найти пределы, не применяя дифференциальное исчисление (правило Лопиталя):

194

286

Посмотреть ответы 2

Ответы на вопрос:

Vikharevaliza

Математика

4,6(18 оценок)

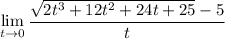б) Сделаем замену (только для удобства) $\sqrt[3]{x} = t+2$ . Тогда предел перепишется в виде $\lim\limits_{t\to 0}\dfrac{\sqrt{2t^3+12t^2+24t+25}-5}{t}$ . Поскольку 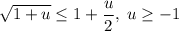$\sqrt{1+u} \leq 1+\dfrac{u}{2},\; u\geq -1$ (докажите самостоятельно), то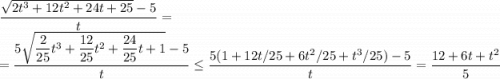 $\dfrac{\sqrt{2t^3+12t^2+24t+25}-5}{t}=\\ = \dfrac{5\sqrt{\dfrac{2}{25}t^3+\dfrac{12}{25}t^2+\dfrac{24}{25}t+1}-5}{t}\leq \dfrac{5(1+12t/25+6t^2/25+t^3/25)-5}{t} = \dfrac{12+6t+t^2}{5}$

С другой стороны, можем умножить и разделить дробь на сопряженное: 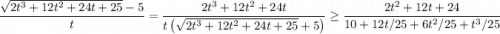$\dfrac{\sqrt{2t^3+12t^2+24t+25}-5}{t} = \dfrac{2t^3+12t^2+24t}{t\left(\sqrt{2t^3+12t^2+24t+25}+5\right)}\geq \dfrac{2t^2+12t+24}{10+12t/25+6t^2/25+t^3/25}$

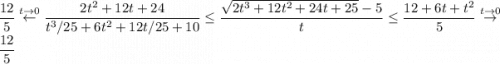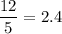В итоге получили $\dfrac{12}{5}\stackrel{t\to 0}{\leftarrow}\dfrac{2t^2+12t+24}{t^3/25+6t^2+12t/25+10}\leq\dfrac{\sqrt{2t^3+12t^2+24t+25}-5}{t}\leq \dfrac{12+6t+t^2}{5}\stackrel{t\to0}{\to} \dfrac{12}{5}$ , следовательно искомый предел равен $\dfrac{12}{5} = 2.4$ .

г) $\lim\limits_{x\to 0}(1+5x)^{\frac{3}{5x}} = \left[\lim\limits_{x\to 0}(1+5x)^{\frac{1}{5x}}\right]^3 = \left[e\right]^3 = e^{3}$ .

vanyazoro

Математика

4,4(81 оценок)

10, т.к это число можно собрать большим кол-вом комбинаций: 3= 1+2 10= 6+4; 5+5;

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Математика

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.