katenautkina69

03.08.2020 19:03

Математика

Есть ответ 👍

Три натуральних числа, сума яких дорівнює 147, є послідовними членами геометричної прогресії з цілим знаменником. Скільки може бути таких трійок чисел?

190

429

Посмотреть ответы 2

Ответы на вопрос:

oreo228123

Математика

4,7(49 оценок)

Всего 8 различных таких троек.

Пошаговое объяснение:

Итак, известно: 3 числа 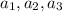a_1, a_2, a_3 такие, что:

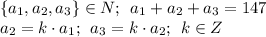
$\{a_1, a_2, a_3\} \in N; \: \: a_1+ a_2+a_3 = 147\\ a_2=k\cdot{a_1}; \: \: a_3=k\cdot{a_2}; \: \: k \in Z$

Найти: число возможных вариантов 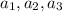a_1, a_2, a_3

Решение: т.к. все 3 числа - члены геом. прогрессии, запишем так:

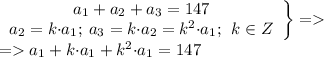
$\left. \begin{array} {c}a_1+ a_2+a_3 = 147\\ a_2=k{\cdot}{a_1}; \: a_3=k{\cdot}{a_2} = {k}^{2}{\cdot}{a_1} ; \: \: k \in Z \end{array} \right \} = \\ = a_1+ {k}{\cdot}{a_1}+{k}^{2}{\cdot}{a_1} = 147 \\$

Теперь преобразуем полученное равенство:

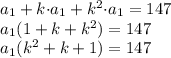
$a_1+ {k}{\cdot}{a_1}+{k}^{2}{\cdot}{a_1} = 147 \\ a_1(1+ {k}+{k}^{2}) = 147 \\ a_1({k}^{2} + k + 1) = 147$

Сделаем замену:

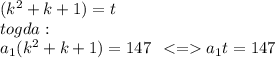
$({k}^{2} + k + 1) = t \\ togda: \\ a_1({k}^{2} + k + 1) = 147 \: \: < = a_1t = 147\\$

Получили произведение 2 множителей, про которые известно, что а1 - натуральное, k - целое..

т.к. а1 - натуральное, 147 - натуральное =>

=> и значение t тоже должно быть натуральным числом.

И, очевидно, значение а1 и t ограничено сочетаниями множителей, на которые можно разложить 147.

Разложим:

147 = 1•3•7•7

Итак, как а, так и t могут принимать значения из множества: {1; 3; 7; 21; 49; 147}

Рассмотрим t. обратная замена;

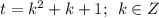
$t = {k}^{2} + k + 1; \: \: k \in Z$

График t(k)= k²+k+1 - парабола, с вершиной в точке 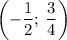$\left(-\dfrac{1}{2};\: \dfrac{3}{4}\right)$ , ветви вверх.

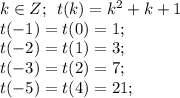
$k \in Z; \: \: t(k) = {k}^{2} + k + 1 \\t( - 1) = t(0) = 1; \\t( - 2) = t(1) = 3; \\ t( - 3) = t(2) = 7 ; \\ t( - 5) = t(4) = 21;$

При значениях t = 49; t = 147 k - не является целым числом, так что они для t не подойдут

Итак: Всего возможно 8 различных значений для k

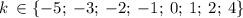
$k \: \in \{ - 5; \: - 3; \: - 2; \: - 1; \: 0; \: 1; \: 2; \: 4 \}$

И для каждого варианта k существует единственный вариант значения а1.

То есть - следовательно, всего различных наборов чисел может быть столько же, сколько различных значений k.

Т. е. всего 8 вариантов различных троек чисел

haruto42

Математика

4,6(11 оценок)

ответ: 14 лет и 7 месяцев

Пошаговое объяснение:

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Математика

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.