Маруся203

18.01.2022 18:57

Есть ответ 👍

В правильной шестиугольной призме, все ребра которой равны 1, найдите угол между прямой AE1 и плоскостью (АВС); между прямой BA1 и плоскостью (AE1D1); между прямой АА1 и плоскостью (АF1D1)

155

309

Посмотреть ответы 2

Ответы на вопрос:

oksyunya

Геометрия

4,8(21 оценок)

Правильная шестиугольная призма - в основании правильный шестиугольник, боковые ребра перпендикулярны основанию.

Угол между прямой и плоскостью - угол между прямой и ее проекцией.

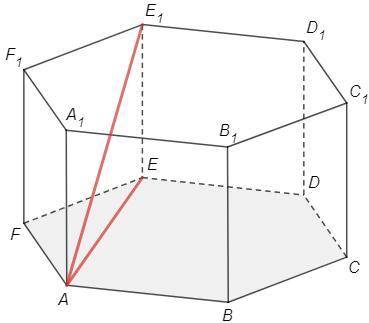
1) EE1⊥(ABC) => AE - проекция наклонной AE1 на плоскость (ABC)

∠E1AE - угол между AE1 и (ABC)

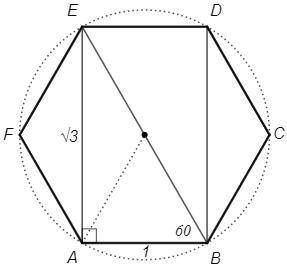
∠ABE=60 (правильный шестиугольник)

AE =AB tg(ABE) =1*tg60 =√3

tg(E1AE) =EE1/AE =1/√3 => ∠E1AE=30°

2) ABDE и ABD1E1 - прямоугольники (ABDE - проекция ABD1E1)

=> AB⊥AE1, AB⊥AE => AB⊥(AEE1)

Опустим A1G⊥AE1

AB⊥(AEE1) => AB⊥A1G

A1G⊥AB, A1G⊥AE1 => A1G⊥(AE1D1)

∠A1BG - угол между BA1 и (AE1D1)

∠E1AE=30 => ∠A1AG=60

A1G =AA1 sin(A1AG) =1*sin60 =√3/2

BA1=√2 (диагональ квадрата)

sin(A1BG) =A1G/BA1 =√3/2 :√2 =√6/4

∠A1BG =arcsin√6/4 ~37,76°

3) Аналогично пункту 2

ACDF и ACD1F1 - прямоугольники => AC⊥(FAA1)

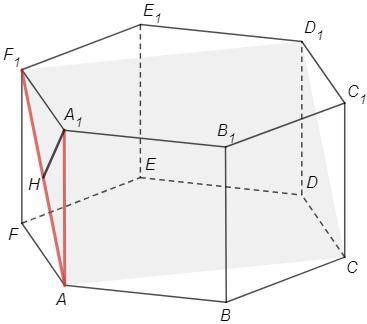
Опустим A1H⊥AF1

AC⊥(FAA1) => AC⊥A1H

A1H⊥AF1, A1H⊥AC => A1H⊥(AF1D1)

∠A1AF1 - угол между AA1 и (AF1D1)

∠A1AF1=45° (AF1 - диагональ квадрата)

valievaalina869

Геометрия

4,4(35 оценок)

не знаю как но попробую

Задай свой вопрос

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.