06.03.2021 21:37

Есть ответ 👍

решите это уравнение всеми , которыми только можно
21+10t-t в квадрате=0

107

373

Посмотреть ответы 3

Ответы на вопрос:

maksimlymar200

Математика

4,6(5 оценок)

1) Решение через дискриминант .

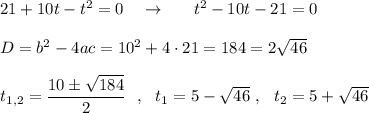
$21+10t-t^2=0\ \ \ \to \ \ \ \ \ t^2-10t-21=0D=b^2-4ac=10^2+4\cdot 21=184=2\sqrt{46}t_{1,2}=\dfrac{10\pm \sqrt{184}}{2}\ \ ,\ \ t_1=5-\sqrt{46}\ ,\ \ t_2=5+\sqrt{46}$

2) Решение с выделения полного квадрата .

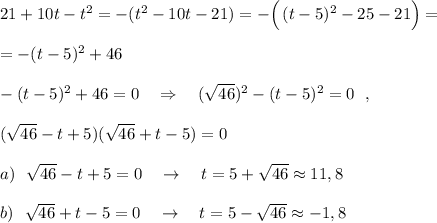
$21+10t-t^2=-(t^2-10t-21)=-\Big(\, (t-5)^2-25-21\Big)==-(t-5)^2+46-(t-5)^2+46=0\ \ \ \Rightarrow \ \ \ (\sqrt{46})^2-(t-5)^2=0\ \ ,(\sqrt{46}-t+5)(\sqrt{46}+t-5)=0a)\ \ \sqrt{46}-t+5=0\ \ \ \to \ \ \ t=5+\sqrt{46}\approx 11,8b)\ \ \sqrt{46}+t-5=0\ \ \ \to \ \ \ t=5-\sqrt{46}\approx -1,8$

3) Решение с теоремы Виета.

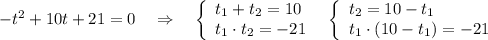
$-t^2+10t+21=0\ \ \ \Rightarrow \ \ \ \left\{\begin{array}{l}t_1+t_2=10\\t_1\cdot t_2=-21\end{array}\righ\ \ \left\{\begin{array}{l}t_2=10-t_1\\t_1\cdot (10-t_1)=-21\end{array}\righ$

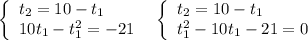
$\left\{\begin{array}{l}t_2=10-t_1\\10t_1-t_1^2=-21\end{array}\righ\ \ \left\{\begin{array}{l}t_2=10-t_1\\t_1^2-10t_1-21=0\end{array}\righ$

Второе уравнение фактически получили такое же, как и было задано . Подобрать корни без решения уравнения через дискриминант в этом случае сложно . Поэтому реально работают первые два решения .

P.S. Легко подобрать корни по теореме Виета , например, для такого уравнения 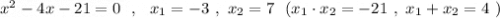$x^2-4x-21=0\ \ ,\ \ x_1=-3\ ,\ x_2=7\ \ (x_1\cdot x_2=-21\ ,\ x_1+x_2=4\ )$ .

4) Графический решения уравнения . Построить параболу и найти точки пересечения с осью ОХ . Но в данном случае точные значения найти практически невозможно. Только приближённые значения : 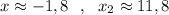$x\approx -1,8\ \ ,\ \ x_2\approx 11,8$ .

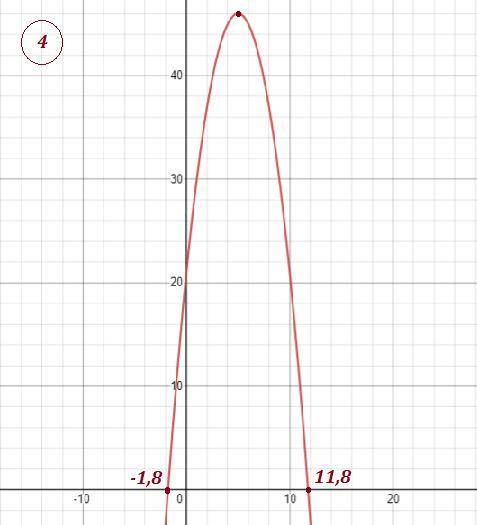
решите это уравнение всеми , которыми только можно21+10t-t в квадрате=0

Alina29052006

Математика

4,7(77 оценок)

Такие квадратные уравнения, как это, можно решить, дополнив их до полного квадрата. Чтобы можно было дополнить уравнение до полного квадрата, оно должно иметь вид x²

+bx=c.

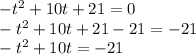
$-t^2+10t+21=0\\-t^2+10t+21-21=-21\\-t^2+10t=-21\\$

Делим обе части на −1.

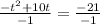
$\frac{-t^2+10t}{-1} =\frac{-21}{-1} \\$

Деление на −1 аннулирует операцию умножения на −1.

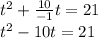
$t^2+\frac{10}{-1} t=21\\t^2-10t=21$

Делим −10, коэффициент члена x, на 2, в результате чего получится −5. Затем добавьте квадрат −5 в обе части уравнения. Это действие сделает левую часть уравнения полным квадратом.

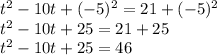
$t^2-10t+(-5)^2=21+(-5)^2\\t^2-10t+25=21+25\\t^2-10t+25=46$

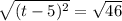
$\sqrt{(t-5)^2} =\sqrt{46} \\$

Упрощаем:

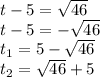
$t-5=\sqrt{46} \\t-5=-\sqrt{46} \\t_{1}=5-\sqrt{46}\\t_{2}=\sqrt{46} +5$

Пошаговое объяснение:

Denze111

Математика

4,6(56 оценок)

24+24=48

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Математика

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.