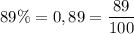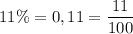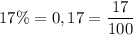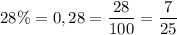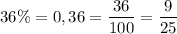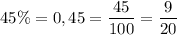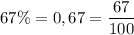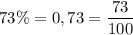goratkin2005

31.01.2023 05:40

Математика

Есть ответ 👍

2 Перетворіть у звичайні дроби. Скоротіть отримані дроби, якщо це можливо. а. 6. В. 17% = 89%= 11%= = г. е. 45% = Д. 28% = 36%= Є. Ж. 67%= 3. 85% = 73% = - Сала

233

433

Посмотреть ответы 2

Ответы на вопрос:

Valik123211

Математика

4,7(71 оценок)

Пошаговое объяснение:

а.

$89\% =0,89= \dfrac{89}{100}$

б.

$11\%=0,11=\dfrac{11}{100}$

в.

$17\%=0,17=\dfrac{17}{100}$

г.

$28\%=0,28=\dfrac{28}{100}=\dfrac{7}{25}$

д.

$36\%=0,36=\dfrac{36}{100}=\dfrac{9}{25}$

е.

$45\%=0,45=\dfrac{45}{100}=\dfrac{9}{20}$

э.

$67\%=0,67=\dfrac{67}{100}$

ж.

$73\%=0,73=\dfrac{73}{100}$

з.

$85\%=0,85=\dfrac{85}{100}=\dfrac{17}{20}$

Løæålø

Математика

4,4(3 оценок)

Восновании правильной четырёхугольной пирамиды sabcd лежит квадрат. bsd-сечение, s=90 градусов, тогда углы в и с равны по 45°, следовательно δbsd-равнобедренный, bs=sd. 1. найдём высоту пирамиды so, которая является также высотой δbsd. эта высота разделила δbsd на два равнобедренных δ bos = δ dos, у которых ob=od=os. пусть ов = od=os = х , диагональ основания bd = 2x следовательно, площадь сечения: 32 = 1/2 * 2х * х x² = 32 х = √32 = 4√2 - это высота пирамиды so (ов = od=os = 4√2) диагональ основания bd = 2 * 4√2 = 8√2 2. найдем сторону основания: ав=√(ов²+ao²)=√(32+32)=√64 = 8 см, 3. для площади боковой грани нужна ещё высота sk этой грани (δsab) - она же апофема. по теореме пифагора апофема sk² = so² + ok² ok = 8/2 = 4 см - это половина стороны основания sk ² = 32 + 16 = 48 sk = √48= 4√3 s = 1/2 * ab * sk s = 1/2 * 8 * 4√3 = 16√3 - площадь одной боковой грани 4. sбоковая = 4 * 16√3 = 64√3 см² sбоковая = 64√3 см²

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Математика

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.