Маша выписывает по порядку на доску натуральные трехзначные числа. Оказалось, что выписанные Дашей числа (их не меньше трех) образуют конечную геометрическую прогрессию, а первое число равно 128.
а) Могла ли Даша выписать на доске число 686?
Б) Могла ли Даша выписать на доске число 496?
в) Какое наибольшее число могла выписать на доске Даша?
Ответы на вопрос:
а) да; б) нет; в) 972
Пошаговое объяснение:
а) Пусть геометрическая прогрессия имеет знаменатель 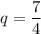 . Тогда получим последовательность
. Тогда получим последовательность 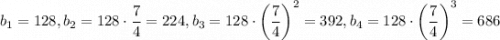 . Число 686 может быть записано на доске.
. Число 686 может быть записано на доске.
б) Заметим, что знаменатель прогрессии q не может быть иррациональным числом: в противном случае второй член прогрессии b₂ = 128q — иррациональное число, что противоречит условию. Значит, q — рациональное число.
Предположим, что 496 является n-ным членом последовательности. Тогда 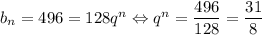 . Поскольку 31 — простое число, оно не является степенью какого-либо другого числа. Значит, n = 1,
. Поскольку 31 — простое число, оно не является степенью какого-либо другого числа. Значит, n = 1, 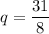 . Тогда получаем геометрическую прогрессию
. Тогда получаем геометрическую прогрессию 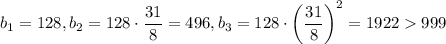 — третий член последовательности не трёхзначный, что противоречит условию. Значит, прогрессии с членом 496 не существует.
— третий член последовательности не трёхзначный, что противоречит условию. Значит, прогрессии с членом 496 не существует.
в) Пусть A — наибольший возможный член геометрической прогрессии, по условию A < 1000. Тогда 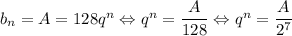 . Число
. Число 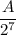 является степенью некоторого рационального числа, значит,
является степенью некоторого рационального числа, значит, 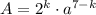 , где k — некоторое целое число из промежутка [0, 7], a — положительное нечётное число. Число представимо в таком виде, поскольку на
, где k — некоторое целое число из промежутка [0, 7], a — положительное нечётное число. Число представимо в таком виде, поскольку на 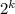 можно сократить, в знаменателе останется
можно сократить, в знаменателе останется 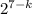 , далее дробь несократима и является степенью n = 7 - k числа q:
, далее дробь несократима и является степенью n = 7 - k числа q: 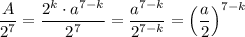 . Значит,
. Значит, 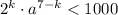 .
.
Переберём все k от 0 до 7:
k = 0: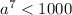 .
. 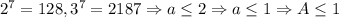 k = 1:
k = 1: 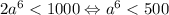 .
. 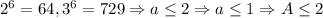 k = 2:
k = 2: 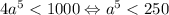 .
. 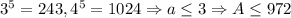 k = 3:
k = 3: 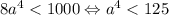 .
. 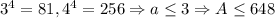 k = 4:
k = 4: 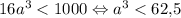 .
. 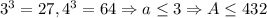 k = 5:
k = 5: 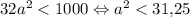 .
. 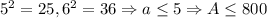 k = 6:
k = 6: 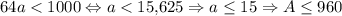 k = 7:
k = 7: 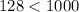 — верно, A = 128.
— верно, A = 128.Наибольшее значение A = 972. Покажем, что оно достигается. Пусть 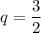 . Тогда
. Тогда 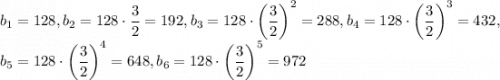
Таким образом, наибольшее число, которое могла выписать Даша — 972.
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Математика
-
Решить задание по алгебре на нормальное распределение ...
 chernov525.10.2021 17:08
chernov525.10.2021 17:08 -
23,9/10 столбиком решите...
 kreatuv41kp06t4215.11.2020 06:40
kreatuv41kp06t4215.11.2020 06:40 -
Сколько сторон у правильного многоугольника, один из внутренних углов...
 sodzirovna19.03.2020 07:48
sodzirovna19.03.2020 07:48 -
A*(a+3)-2*(a+3) ax-ay+5x-5y...
 Po99920.10.2022 19:51
Po99920.10.2022 19:51 -
2. Длина стороны ква рата и длина каждого прямоугольника равны 40 мм....
 милка57809.06.2022 07:53
милка57809.06.2022 07:53 -
Вычислите определённый интеграл с точностью до 0.001 ...
 lorik0203.02.2023 01:57
lorik0203.02.2023 01:57 -
Решить задание по алгебре на дисперсию показательного распределения...
 arsenkam01.07.2021 23:49
arsenkam01.07.2021 23:49 -
Множество Ф состоит из точек, координаты которых (x,y) в прямоугольной...
 Сашуньк29.07.2020 00:25
Сашуньк29.07.2020 00:25 -
решить задачу:. Наименьшее общее кратное двух натуральных чисел больше...
 saralis24.07.2020 07:22
saralis24.07.2020 07:22 -
До магазину привезли 28 кг печива та вафель. Маса печива складає чверть...
 спаситепомогите11117.06.2023 15:37
спаситепомогите11117.06.2023 15:37

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.
