Математика: 12cos50°+6cos70° все это поделить на √3sin70° . как решать?

Psix73

10.01.2023 10:00

Математика

Есть ответ 👍

12cos50°+6cos70° все это поделить на √3sin70° .
как решать?

297

476

Посмотреть ответы 2

Ответы на вопрос:

акакий27

Математика

4,5(57 оценок)

ответ: 6

Пошаговое объяснение:

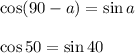
$\cos(90-a) =\sin a \ \cos50=\sin40$

$\displaystyle \frac{12\cos50 +6 \cos 70 }{\sqrt{3}\sin70 }} =\frac{12\sin40+6\cos70+6\sqrt{3} \sin 70-6\sqrt{3} \sin 70 }{\sqrt{3}\sin70}= \frac{12\sin40 + ( 6 \cos 70 + 6\sqrt{3}\sin70)}{\sqrt{3}\sin70} -\frac{6\cdot \sqrt{3}\sin70}{\sqrt{3}\sin70} = \frac{12\sqrt{3}\sin70 }{\sqrt{3}\sin70 } -6 =12-6 =\boxed{6}$

Упростим выражение

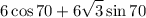
$\displaystyle 6 \cos 70 + 6\sqrt{3}\sin70$

Вынесем 12 за скобки

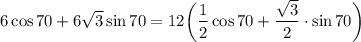
$\displaystyle 6 \cos 70 + 6\sqrt{3}\sin70=12 \bigg(\frac{1}{2} \cos70 +\frac{\sqrt{3} }{2}\cdot \sin70 \bigg)$

Подставим

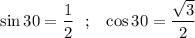
$\sin 30=\dfrac{1}{2} ~~ ;~~ \cos30=\dfrac{\sqrt{3} }{2}$

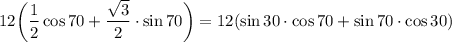
$\displaystyle 12 \bigg(\frac{1}{2} \cos70 +\frac{\sqrt{3} }{2}\cdot \sin70 \bigg)=12(\sin30\cdot \cos70 +\sin70\cdot \cos30 )$

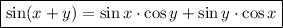
$\boxed{\sin(x+y)=\sin x \cdot \cos y +\sin y \cdot \cos x}$

Тогда

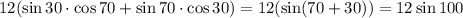
$\displaystyle 12(\sin30\cdot \cos70 +\sin70\cdot \cos30 )=12(\sin(70+30))=12\sin100$

Дальше в числителе

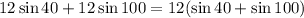
$\displaystyle 12\sin40+12\sin 100 =12(\sin40 + \sin100)$

Воспользуемся формулой

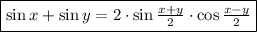
$\boxed{\sin x+\sin y=2 \cdot \sin\tfrac{x+y}{2} \cdot \cos\tfrac{x-y}{2}}$

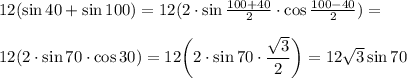
$12(\sin40 + \sin100)=12(2\cdot \sin\frac{100+40}{2}\cdot \cos\frac{100-40}{2} )= 12(2\cdot \sin 70 \cdot \cos30)=12\bigg(2\cdot \sin 70\cdot \dfrac{\sqrt{3} }{2} \bigg)=12\sqrt{3}\sin70$

Nice1111111111111

Математика

4,8(50 оценок)

60% от исходного - 0,6x

0,6x - 0,2 * 0,6x = 0,48x

ответ: 48%

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Математика

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.