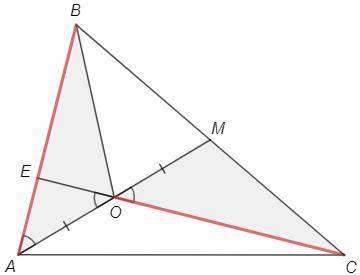
На сторонах AB и BC треугольника ABC отметили соответсвенно точки E и M так, что отрезок CE пересекает отрезок AM в его середине — точка O. Известно, что AB=CO и EA=EO. Докажите, что отрезок AM — медиана треугольника ABC.

162

266

Посмотреть ответы 2

Ответы на вопрос:

Svetiksmail5454

Геометрия

4,6(92 оценок)

EA=EO, △AEO - р/б => ∠EAO=∠EOA (углы при основании)

∠EOA=∠COM (вертикальные)

=> ∠EAO=∠COM

AB=CO, AO=OM (по условию)

△BAO=△COM (по двум сторонам и углу между ними)

BO=CM, ∠AOB=∠OMC

∠BOM=∠BMO (смежные с равными) => △OBM - р/б, BO=BM

=> CM=BM, AM - медиана

Matthieu5401

Геометрия

4,4(72 оценок)

1 - Б;

2 - Г;

3 - А;

4 - В.

Задай свой вопрос

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.