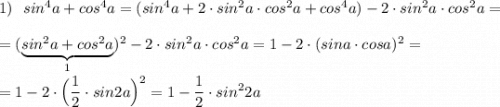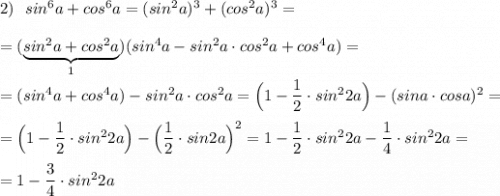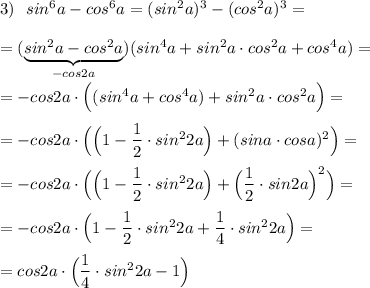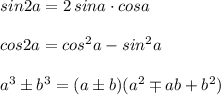Регистрация Спросить otvet5GPT
Unknown112
19.07.2022 20:04
Алгебра
Есть ответ 👍

1)sin^4альфа +cos^4альфа
2)sin^6 альфа +-cos^6 альфа

186
449
Посмотреть ответы 2

Ответы на вопрос:

VTKOF
VTKOF
4,5(48 оценок)

1)\ \ sin^4a+cos^4a=(sin^4a+2\cdot sin^2a\cdot cos^2a+cos^4a)-2\cdot sin^2a\cdot cos^2a==(\underbrace{sin^2a+cos^2a}_{1})^2-2\cdot sin^2a\cdot cos^2a=1-2\cdot (sina\cdot cosa)^2==1-2\cdot \Big(\dfrac{1}{2}\cdot sin2a\Big)^2=1-\dfrac{1}{2}\cdot sin^22a

2)\ \ sin^6a+cos^6a=(sin^2a)^3+(cos^2a)^3==(\underbrace{sin^2a+cos^2a}_{1})(sin^4a-sin^2a\cdot cos^2a+cos^4a)==(sin^4a+cos^4a)-sin^2a\cdot cos^2a=\Big(1-\dfrac{1}{2}\cdot sin^22a\Big)-(sina\cdot cosa)^2==\Big(1-\dfrac{1}{2}\cdot sin^22a\Big)-\Big(\dfrac{1}{2}\cdot sin2a\Big)^2=1-\dfrac{1}{2}\cdot sin^22a-\dfrac{1}{4}\cdot sin^22a==1-\dfrac{3}{4}\cdot sin^22a

3)\ \ sin^6a-cos^6a=(sin^2a)^3-(cos^2a)^3==(\underbrace{sin^2a-cos^2a}_{-cos2a})(sin^4a+sin^2a\cdot cos^2a+cos^4a)==-cos2a\cdot \Big((sin^4a+cos^4a)+sin^2a\cdot cos^2a\Big)==-cos2a\cdot \Big(\Big(1-\dfrac{1}{2}\cdot sin^22a\Big)+(sina\cdot cosa)^2\Big)==-cos2a\cdot \Big(\Big(1-\dfrac{1}{2}\cdot sin^22a\Big)+\Big(\dfrac{1}{2}\cdot sin2a\Big)^2\Big)==-cos2a\cdot \Big(1-\dfrac{1}{2}\cdot sin^22a+\dfrac{1}{4}\cdot sin^22a\Big)==cos2a\cdot \Big(\dfrac{1}{4}\cdot sin^22a-1\Big)

Формулы:

sin2a=2\, sina\cdot cosacos2a=cos^2a-sin^2aa^3\pm b^3=(a\pm b)(a^2\mp ab+b^2)

999997675656
999997675656
4,4(66 оценок)

разложить на множители:

а) сначало выносим у

у(у^2-49)=у((у-7)(у+7))

б) не знаю

найдите значение выражения

а^2-4bc если а=6 в=-11 с=-10

сразу подставляем

6*6-4*(-11)*(-10)=36-440=-404 вроде так)

выражения 

= (а^2-1)^2+а^2-1= а^4-2а^2+1+а^2-1 = а^4-а^2

докажите тождество

х^2-2ху+у^2+х^2+2ху+у^2=2х^2+2у^2

2х^2+2у^2=2х^2+2у^2

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS