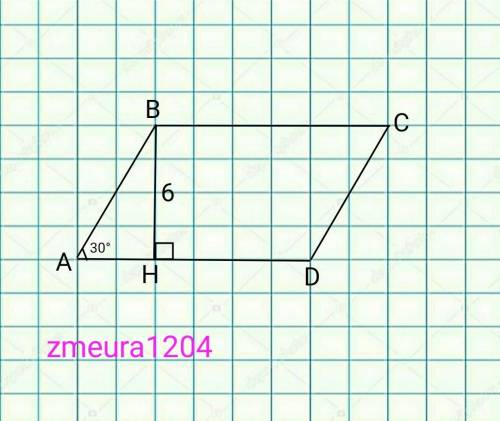
1. Периметр параллелограмма ABCD равен 56 см. Из вершины угла В, равного 150°, на сторону AD проведена высота ВН, рав- ная 6 см. Найдите площадь параллелограмма ABCD.

278

443

Посмотреть ответы 2

Ответы на вопрос:

QeenNahimi05062

Геометрия

4,7(46 оценок)

96см²

Объяснение:

Сумма углов прилежащих к одной стороне параллелограма равна 180°

<В+<А=180°

<А=180°-<В=180°-150°=30°

∆АВН- прямоугольный треугольник

АВ=2*ВН=2*6=12см катет против угла <А=30°.

Р=2(АВ+ВС). →

ВС=Р:2-АВ=56:2-12=16см

AD=BC, свойство параллелограма

S=BH*AD=16*6=96см²

1. Периметр параллелограмма ABCD равен 56 см. Из вершины угла В, равного 150°, на сторону AD проведе

Lãkomkã01

Геометрия

4,4(84 оценок)

1. теорема 1 (первый признак параллельности) если при пересечении двух прямых третьей накрест лежащие(внутренние или внешние) углы равны, то такие прямые параллельны. доказательство: дано: прямые ab, cd и mn; угол 1= угол 2 . требуется доказать: ab||cd. возьмем точку o — середину mn и проведем ok перпендикулярно cd. докажем, что ok перпендикулярно ab. треугольник okn= треугольник olm (по стороне и двум прилежащим углам). в них угол olm= углу okn. но угол okn = 180 градусов. следовательно, kl перпендикулярно ab: ab||cd. если будет дано, что равны внешние накрест лежащие углы, то обязательно будут равны и внутренние накрест лежащие углы. 2. поскольку сумма всех углов треугольника равна 180 градусам, то 180 - 110 = 70 70 / 2 = 35 ответ: углы треугольника 35 и 35.

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.