Алгебра: Решить данные неравенства : (x+4)^2 0 x^2+4 0 x^2+3x 0

Andrey26022002

25.04.2020 06:36

Алгебра

Есть ответ 👍

Решить данные неравенства : (x+4)^2<0 x^2+4<0 x^2+3x<0

250

256

Посмотреть ответы 3

Ответы на вопрос:

петя1023

Алгебра

4,6(70 оценок)

Объяснение:

№1

(x+4)^2

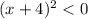
Квадрат действительного числа всегда больше нуля или равен нулю.

Равен нулю в том случае если неравенство нестрогое .

В этом же случае неравенство строгое .

Из чего исходя у данного неравенства нет решений .

№2

x^2+4

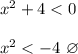
Аналогично и здесь

Нет решений

№3

x^2+3x

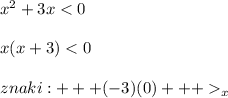
В этом же случае решение есть

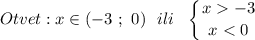
$Otvet: x \in (-3 \ ; \ 0 ) \ \ ili \ \ \displaystyle \left \{ {{x-3} \atop {x$

busiginaev2015

Алгебра

4,7(78 оценок)

В решении.

Объяснение:

Решить данные неравенства : (x+4)^2<0 x^2+4<0 x^2+3x<0;

1) (x + 4)² < 0

х² + 8х + 16 < 0

Приравнять к нулю и решить квадратное уравнение:

х² + 8х + 16 = 0

D=b²-4ac = 64 - 64 = 0 √D=0

х=(-b±√D)/2a

х=(-8±0)/2

х = -4.

Уравнение квадратичной функции, график - парабола. Значение х = -4 указывает на то, что парабола "стоит" на оси Ох в точке х= -4, весь график выше оси Ох, значит, у < 0 не существует.

Неравенство не имеет решения.

2) x² + 4 < 0

Приравнять к нулю и решить квадратное уравнение:

x² = -4

Уравнение не имеет действительных корней.

Неравенство не имеет решения.

3) x² + 3x < 0

Приравнять к нулю и решить неполное квадратное уравнение:

x² + 3x = 0

х(х + 3) = 0

х₁ = 0;

х + 3 = 0

х₂ = -3;

Уравнение квадратичной функции, график парабола, ветви направлены вверх, пересекают ось Ох в точках х= 0 и х= -3.

На промежутке от х= -3 до х=0 у<0 (парабола ниже оси Ох).

Решения неравенства: х∈(-3; 0).

Неравенство строгое, скобки круглые.

Danila240899

Алгебра

4,6(62 оценок)

√2+√17≈0,414+4,123=4,537≈4,5.

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Алгебра

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.