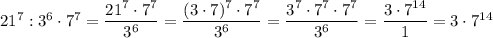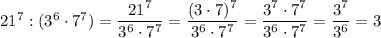Регистрация Спросить otvet5GPT
Danielkz02
10.05.2020 05:12
Алгебра
Есть ответ 👍

Обчисліть: 21 у 7 степені : 3 у 6 степені • 7 у 7 степені

286
353
Посмотреть ответы 3

Ответы на вопрос:

link21
link21
4,4(100 оценок)

21⁷=1 801 088 541

3⁶=729

7⁷=823 543

valenok18XD
valenok18XD
4,4(31 оценок)

Свойства степеней:  \boxed{\ (a\cdot b)^{k}=a^{k}\cdot b^{k}\ \ ,\ \ a^{n}\cdot a^{k}=a^{n+k}\ \ ,\ \ \dfrac{a^{n}}{a^{k}}=a^{n-k}\ }   .

21^7:3^6\cdot 7^7=\dfrac{21^7\cdot 7^7}{3^6}=\dfrac{(3\cdot 7)^7\cdot 7^7}{3^6}=\dfrac{3^7\cdot 7^7\cdot 7^7}{3^6}=\dfrac{3\cdot 7^{14}}{1}=3\cdot 7^{14}

Возможно условие такое:

21^7:(3^6\cdot 7^7)=\dfrac{21^7}{3^6\cdot 7^7}=\dfrac{(3\cdot 7)^7}{3^6\cdot 7^7}=\dfrac{3^7\cdot 7^7}{3^6\cdot 7^7}=\dfrac{3^7}{3^6}=3

РенаКОСЫРЕВА
РенаКОСЫРЕВА
4,8(74 оценок)
Одз {x²-x-3> 0 {2x²+x-3> 0 {x²-2≠0 1)x²-x-3> 0 d=1+12=13 x1=(1-√13)/2 u x2=(1+√13)/2 x< (1-√13)/2 u x> (1+√13)/2 2)2x²+x-3> 0 d=1+24=25 x1=(-1-5)4=-1,5 u x=(-1+5)/4=1 x< -1,5 u x> 1 3)x²-2≠0 x²≠2 x≠-√2 u x≠√2 x∈(-∞; -1,5) u ((1+√13)/2; ∞) log(3)[(x²-x-3)(2x²+x-3)/(x²-2)²]≥log(3)(9/4) [(x²-x-3)(2x²+x-3)/(x²-2)²]≥9/4 [(x²-x-3)(2x²+x-3)/(x²-2)²]-9/4≥0 (8x^4+4x³-12x²-8x³-4x²+12x-24x²+-12x+36-9x^4+36x²-36)/4(x²-2)²≥0 (-x^4-4x³-4x²)/4(x²-2)²≥0 -x²(x²+4x+4)/4(x²-2)²≥0 x²(x+2)²/4(x²-2)²≤0 x=0∉одз x=-2∉одз ответ нет решения

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

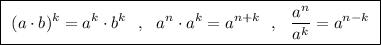Подпишись на наш телеграмм канал

GTP TOP NEWS