Регистрация Спросить otvet5GPT
nezervillager
03.10.2022 03:29
Алгебра
Есть ответ 👍

за решение с ответами,нужно до 14 числа

116
336
Посмотреть ответы 3

Ответы на вопрос:

Ксюша00111
Ксюша00111
4,5(48 оценок)

ответ: во вложении.

Объяснение: там же


за решение с ответами,нужно до 14 числа
за решение с ответами,нужно до 14 числа
yvtcrvt
yvtcrvt
4,6(49 оценок)

\displaystyle 5)\ \ tgx=\dfrac{2}{\sqrt5}a)\ \ 1+tg^2x=\frac{1}{cos^2x}\ \ \ \Rightarrow \ \ \ cos^2x=\frac{1}{1+tg^2x}=\frac{1}{1+\frac{4}{5}}=\frac{5}{9}x\in \Big(\pi \ ;\ \frac{3\pi }{2}\ \Big)\ \ \Rightarrow \ \ cosx0\ ,{}\qquad \qquad \qquad \qquad \qquad cos\frac{x}{2}

b)\ \ \displaystyle sin2x=2\cdot sinx\cdot cosx=2\cdot \Big(-\frac{2}{3}\Big)\cdot \Big(-\frac{\sqrt5}{3}\Big)=\frac{4\sqrt5}{9}\ \ ,cos2x=cos^2x-sin^2x=\frac{5}{9}-\frac{4}{9}=\frac{1}{9}tg2x=\frac{sin2x}{cos2x}=\frac{4\sqrt5/9}{1/9}=4\sqrt5

\displaystyle c)\ \ sin^2\frac{x}{2}=\frac{1-cosx}{2}=\frac{1+\frac{\sqrt5}{3}}{2}=\frac{3+\sqrt5}{6}\ \ ,\ \ \ sin\frac{x}{2}=+\sqrt{\frac{3+\sqrt5}{6}}cos\frac{x}{2}=-\sqrt{1-sin^2\frac{x}{2}}=-\sqrt{1-\frac{3+\sqrt5}{6}}=-\sqrt{\frac{3-\sqrt5}{6}}tg\frac{x}{2}=\frac{sin\frac{x}{2}}{cos\frac{x}{2}}=-\frac{\sqrt{3+\sqrt5}}{\sqrt{3-\sqrt5}}=-\sqrt{\frac{(3+\sqrt5)^2}{9-5}}=-\frac{3+\sqrt5}{2}

6)\ \ y=2\, cos\Big(x-\dfrac{x}{4}\Big)\ \ ,\ \ \ x\in \Big[-\dfrac{\pi}{2}\ ;\ \pi \ \Big]

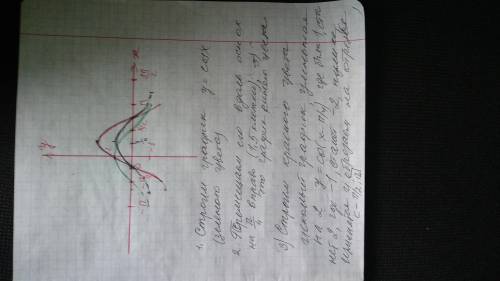
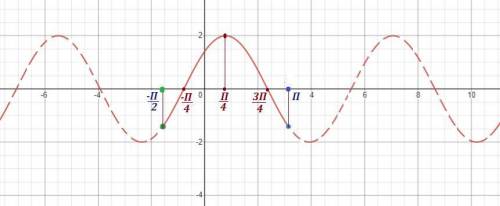
График получаем путём сдвига графика y=cosx  на П/4 единицы

вправо вдоль оси ОХ и растяжением его в 2 раза вдоль оси ОУ .

Затем оставляем только ту часть графика, которая проецируется на заданный сегмент . На рисунке он начерчен сплошной линией .

Нули функции будут при х= -П/4 и х=3П/4 .


за решение с ответами,нужно до 14 числа
Gufka965
Gufka965
4,4(94 оценок)
Можете сфотать а то не понятно

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS