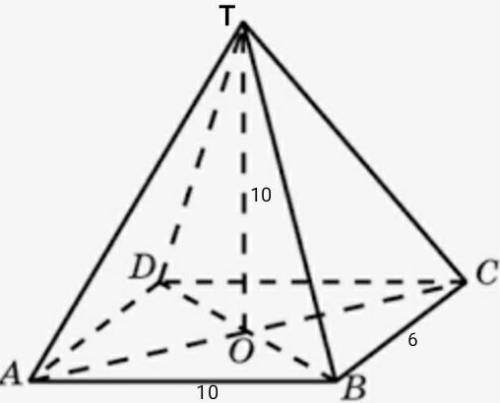
длины сторон прямоугольника равны 10 и 6. через точку о пересечения диагоналей прямоугольника проведен перпендикуляр к плоскости прямоугольника от равный 10. найдите расстояние от точки т до вершин прямоугольника.

143

269

Посмотреть ответы 2

Ответы на вопрос:

mstella2003

Геометрия

4,8(86 оценок)

√134 ед

Объяснение:

∆АСВ- прямоугольный треугольник

По теореме Пифагора

АС=√(АВ²+ВС²)=√(10²+6²)=√136=2√34 ед

АС=DB, диагонали прямоугольника.

ОВ=DB/2=2√34/2=√34 ед.

∆ТОВ- прямоугольный треугольник

По теореме Пифагора

ТВ=√(ТО²+ОВ²)=√(10²+(√34)²)=√134 ед.

длины сторон прямоугольника равны 10 и 6. через точку о пересечения диагоналей прямоугольника провед

denisbainazov

Геометрия

4,4(30 оценок)

1. < cbm=< amb как накрест лежащие углы при пересечении двух параллельных прямых вс и ad секущей вм. но < cbm=< abm, т.к. вм - биссектриса, значит < amb=< abm, и треугольник авм равнобедренный (углы при его основании вм равны между собой). ав=ам. < ckd=< adk как накрест лежащие углы при пересечении двух параллельных прямых вс и ad секущей kd. но < adk=< cdk, т.к. dk - биссектриса, значит < ckd=< cdk. треугольник ckd получается равнобедренным с равными углами при его основании dk. cd=ck т.к. abcd - параллелограмм, то ав=cd. но мы выше вывели, что ав=ам, а cd=cк, значит ам=ск треугольники амв и ckd получаются равны по двум сторонам и углу между ними: ав=cd, ам=ск, углы а и с равны как противоположные углы параллелограмма. 2. вк=вс-ск, dm=ad-ам. поскольку вс=ad, а ск=ам (как равные соответственные стороны равных треугольников амв и ckd), то вк=dm. эти отрезки лежат на параллельных сторонах вс и ad, значит, они также параллельны. значит, bkdm - параллелограмм (две стороны равны и параллельны), следовательно, вм ii dk.

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.