Регистрация Спросить otvet5GPT
nozdracheva95
04.01.2020 04:25
Алгебра
Есть ответ 👍

решить задачу при каком значении a уровнение имеет бесконечно множество корней

275
469
Посмотреть ответы 2

Ответы на вопрос:

дагмгп
дагмгп
4,6(50 оценок)

Такого значения параметра а не существует!

Объяснение:

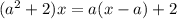
(a^{2} + 2)x = a(x - a) + 2

Линейное уравнение будет иметь бесконечное множество корней если оно в общем виде записывается как: 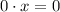0 \cdot x = 0

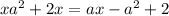
xa^{2} + 2x = ax - a^{2} + 2

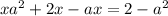
xa^{2} + 2x - ax =2 - a^{2}

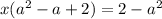
x(a^{2} - a + 2) =2 - a^{2}

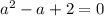
a^{2} -a + 2 = 0

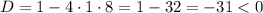D = 1 - 4 \cdot 1\cdot 8 = 1 - 32 = -31 < 0 - нет действительных корней

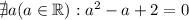\nexists a (a \in \mathbb R): a^{2} - a + 2 =0 Следовательно условие 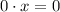0 \cdot x = 0 - не выполняется и таких а нет.

Mila2019
Mila2019
4,4(96 оценок)

Метод интервалов — это специальный алгоритм, предназначенный для решения сложных неравенств вида f(x) > 0. Алгоритм состоит из 5 шагов:

Решить уравнение f(x) = 0. Таким образом, вместо неравенства получаем уравнение, которое решается намного проще;

Отметить все полученные корни на координатной прямой. Таким образом, прямая разделится на несколько интервалов;

Найти кратность корней. Если корни четной кратности, то над корнем рисуем петлю. (Корень считается кратным, если существует четное количество одинаковых решений)

Выяснить знак (плюс или минус) функции f(x) на самом правом интервале. Для этого достаточно подставить в f(x) любое число, которое будет правее всех отмеченных корней;

Отметить знаки на остальных интервалах, чередуя их.

После этого останется лишь выписать интервалы, которые нас интересуют. Они отмечены знаком «+», если неравенство имело вид f(x) > 0, или знаком «−», если неравенство имеет вид f(x) < 0.

В случае с нестрогими неравенствами( ≤ , ≥) необходимо включить в интервалы точки, которые являются решением уравнения f(x) =

Объяснение:

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS