Геометрия: 7-10 задачи. Теорема синусов

Mild06

04.05.2023 09:45

Есть ответ 👍

7-10 задачи. Теорема синусов

198

473

Посмотреть ответы 2

53490

Геометрия

4,5(58 оценок)

Насчет формул теоремы синусов, я писал в другом вашем вопросе, поэтому сразу напишу решения задачи.

Сумма внутренних углов треугольника 180°.

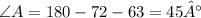
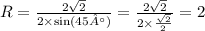
$\angle A = 180 - 72 - 63 = 45°$

$R = \frac{2 \sqrt{2} }{2 \times \sin(45°) } = \frac{2 \sqrt{2} }{2 \times \frac{ \sqrt{2} }{2} } = 2$

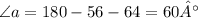
$\angle a = 180 - 56 - 64 = 60°$

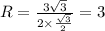
$R = \frac{3 \sqrt{3} }{2 \times \frac{ \sqrt{3} }{2} } = 3$

Синус внешнего угла треугольника равна синусу внутреннего, поэтому sinA=4/5.

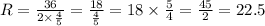
$R = \frac{36}{2 \times \frac{4}{5} } = \frac{18}{ \frac{4}{5} } = 18 \times \frac{5}{4} = \frac{45}{2} = 22.5$

10.

Косинус внешнего угла равен отрицательному косинусу внутреннего, то есть cosA=-5/13.

Сумма квадратов синуса и косинуса равна одному, по этому находим синус

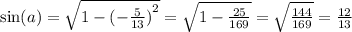
$\sin(a) = \sqrt{1 - {( - \frac{5}{13}) }^{2} } = \sqrt{1 - \frac{25}{169} } = \sqrt{ \frac{144}{169} } = \frac{12}{13}$

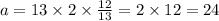
$a = 13 \times 2 \times \frac{12}{13} = 2 \times 12 = 24$

BC=24.

dadada0

Геометрия

4,4(74 оценок)

12+12=24- две сторони

60 - 24=36-1 сторона

и теперь по этим сторонам найди периметр

рада была

Задай свой вопрос

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.