Ответы на вопрос:
Следует, во-первых, показать, что 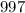 является простым числом. Делается это так: у любого составного числа
является простым числом. Делается это так: у любого составного числа 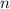 есть хотя бы один делитель, отличный от единицы, не превосходящий
есть хотя бы один делитель, отличный от единицы, не превосходящий 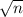 . В самом деле, если такого делителя нет, то найдутся два делителя, больших
. В самом деле, если такого делителя нет, то найдутся два делителя, больших 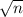 , а это невозможно. Поэтому достаточно проверить наличие делителей от
, а это невозможно. Поэтому достаточно проверить наличие делителей от 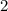 до
до 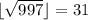 . Из них нужно проверять только простые:
. Из них нужно проверять только простые: 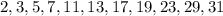 , что сделать уже совсем нетрудно.
, что сделать уже совсем нетрудно.
По малой теореме Ферма мы знаем, что 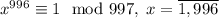 .
. 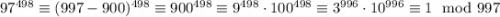 .
.
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Математика
-
Условие к 6 коробок печенья и 5 коробок конфет весят 6кг 200г. сколько...
 1Err0r129.09.2021 01:48
1Err0r129.09.2021 01:48 -
Сколько будет одна целая три четвёртый отнять одну шестую?...
 alyo7na08.11.2020 13:58
alyo7na08.11.2020 13:58 -
На стадионе проходит развлекательная программа ,длительность которой...
 МариКэт126.11.2020 21:36
МариКэт126.11.2020 21:36 -
Вящике 10 перенумерованных шаров с номерами от 1 до 10. вынули один шар....
 students1716.06.2021 15:25
students1716.06.2021 15:25 -
Пассажир метро, стоящий на ступеньке эскалатора, поднимается вверх за...
 Михона23.10.2020 14:17
Михона23.10.2020 14:17 -
Найди делитель если делитель равен 18 неполное частное 4 а остаток 11...
 abakanilaha13.12.2020 04:27
abakanilaha13.12.2020 04:27 -
На маленькой кассете записано 6 песни а на большой на 4 песня больше...
 angelnoya122.07.2022 23:19
angelnoya122.07.2022 23:19 -
Лифт поднимается с первого этажа на третий за 6секунд. за сколько секунд...
 JafarSafarov07.04.2020 06:21
JafarSafarov07.04.2020 06:21 -
Запиши властивості піску, глини й крейди. пісок. глина. крейда...
 Raul02050718.10.2021 05:38
Raul02050718.10.2021 05:38 -
Решите уравнение с пропорции: 2/5=6/x+3...
 bella8002.02.2020 20:07
bella8002.02.2020 20:07

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

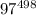 -1 делится на 997
-1 делится на 997