Геометрия: 4-6 задача, теорема синусов

iga5

11.06.2023 23:47

Геометрия

Есть ответ 👍

4-6 задача, теорема синусов

251

488

Посмотреть ответы 2

Ответы на вопрос:

rayhan8888

Геометрия

4,4(26 оценок)

Теорема синусов гласит, что стороны треугольника пропорциональны синусам противолежащих углов, то есть:

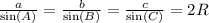
$\frac{a}{ \sin(A) } = \frac{b}{ \sin(B) } = \frac{c}{ \sin(C) } = 2R$

В нашем случае a=BC, b=AC, c=AB, а R — радиус описанной окружности.

BC=6√3, AB=6√2, ∠A=60°

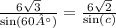
$\frac{6 \sqrt{3} }{ \sin(60°) } = \frac{6 \sqrt{2} }{ \sin(c) }$

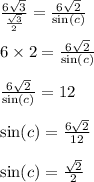
$\frac{6 \sqrt{3} }{ \frac{ \sqrt{3} }{2} } = \frac{6 \sqrt{2} }{ \sin(c) } \\ \\ 6 \times 2 = \frac{6 \sqrt{2} }{ \sin(c) } \\ \\ \frac{6 \sqrt{2} }{ \sin(c) } = 12 \\ \\ \sin(c) = \frac{6 \sqrt{2} }{12} \\ \\ \sin(c) = \frac{ \sqrt{2} }{2}$

Угол C может быть 45° или 135° (по таблице синусов), но так как у треугольника сумма внутренних углов 180°, а 135°+60°=195°, что уже больше 180°, поэтому угол С равен 45°. А еще по условию треугольник остроугольный, а 135° — тупой угол.

BC=4√3, A=60°. R-?

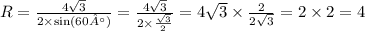
$R = \frac{4 \sqrt{3} }{2 \times \sin(60°) } = \frac{4 \sqrt{3} }{2 \times \frac{ \sqrt{3} }{2} } = 4 \sqrt{3} \times \frac{2}{2 \sqrt{3} } = 2 \times 2 = 4$

Радиус описанной окружности 4.

R=14, A=30°, BC-?

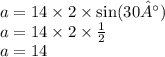
$a = 14 \times 2 \times \sin(30°) \\ a = 14 \times 2 \times \frac{1}{2} \\ a = 14$

BC=14

lidakirillina

Геометрия

4,5(48 оценок)

Высота делит равнобедренный треугольник на равных прямоугольных треугольника, в которых является одним из катетов, также делит основание на две равных части. треугольник должен быть равносторонним. значит гипотенуза х, один катет 97 корней из 3, а второй 0,5х(т.к половина). по теореме пифагора: (0,5х)^2+(97корней из 3)^2=х^2 0,25х^2+28227=х^2 28227=0,75х^2 х^2=37636 х=194 сторона р=194*3=582.

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.