Математика: Найдите:x+2y ,если (x-4)^2+(x-y^2)^2=0

flowersemenova2

10.09.2022 20:09

Математика

Есть ответ 👍

Найдите:x+2y ,если (x-4)^2+(x-y^2)^2=0

123

215

Посмотреть ответы 2

Ответы на вопрос:

supermichail29

Математика

4,8(52 оценок)

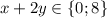
$x+2y \in \{0;8\}$

Пошаговое объяснение:

Очевидно, что, т.к. а² ≥ 0 для любых действительных значений а, => сумма квадратов может быть равна нулю тогда и только тогда, когда все слагаемые равны нулю, а соответственно, нулю равны и все возводимые в квадрат выражения:

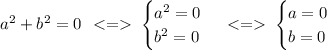
$a^{2} + b^{2} = 0 \: \: < = \: \begin{cases}a^{2} = 0 \\ b^{2} = 0 \end{cases} \: < = \: \begin{cases}a = 0 \\ b = 0 \end{cases}$

В нашем случае получаем следующее:

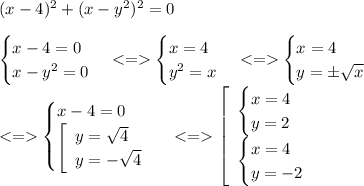
$(x-4)^2+(x-y^2)^2=0 \\ \\ \begin{cases} x - 4 = 0 \\ x - {y}^{2} = 0 \end{cases} < = \begin{cases} x = 4 \\ {y}^{2} = x \end{cases} < = \begin{cases} x = 4 \\ {y} = \pm \sqrt{x} \end{cases} \\ < = \begin{cases} x - 4 = 0 \\ \left[ \begin{array}{l}y= \sqrt{4}\\ y = - \sqrt{4} \end{array} \right. \end{cases} < = \left[ \begin{array}{l}\begin{cases} x= 4 \\ y= 2 \end{cases}\\ \begin{cases} x= 4 \\ y= - 2 \end{cases} \end{array} \right.$

Получилось 2 пары (х, у):

(4; 2) и (4; -2)

Соответственно и выражение

х + 2у

может принимать 2 значения:

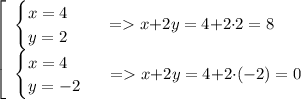
$\left[ \begin{array}{l}\begin{cases} x= 4 \\ y= 2 \end{cases} \: \: \: \: \: = x{ +} 2y = 4 {+ }2{ \cdot}2 = 8\\ \begin{cases} x= 4 \\ y= - 2 \end{cases}\: \: = x{ +} 2y = 4 {+ }2{ \cdot}({ - 2}) = 0 \end{array} \right.$

Поэтому получаем 2 ответа:

ответ

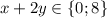
$x+2y \in \{0;8\}$

ЗВЕР4ЁК

Математика

4,8(16 оценок)

3/5. сокращаем на 630 1/5 сокращаем на 1815

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Математика

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.