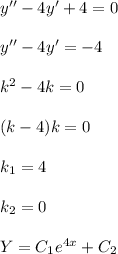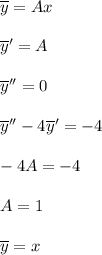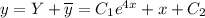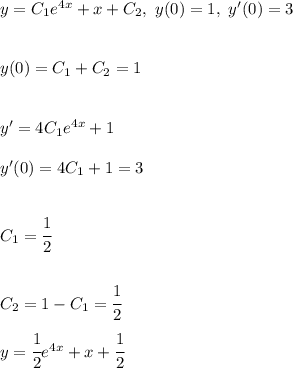Найти общее и частное решение дифференциального уравнения второго порядка: y′′ − 4y′ + 4 = 0 (0) = 1; '(0) = 3
Ответы на вопрос:
y′′ − 4y′ + 4 = 0
Решим характеристическое уравнение
к²-4к=0;
к*(к-4)=0
к₁=0; к₁=4;
общее решение соответствующего однородного уравнения имеет вид
уобщ. =с₁*е^(0*x)+c₂e^(4х), или уобщ.=с₁+c₂e^(4х)
т.к. y′′ − 4y′=- 4 , то частное решение ищем по правой части, которая представляет из себя многочлен нулевой степени, учитав, что 0-однократный корень характеристического уравнения. значит.
уч.=Ах,
у'=А,
у''=0
для определения А , подставим уч.=Ах, у'=А, у''=0 в исходное уравнение,
-4А=-4, значит, А=1, уч.=х,
зная, что общее решение неоднородного уравнения равно сумме общего решения однородного и частного решения неоднородного,
получим Y=уо.o+yо.н., подставим найденные уо.o и yо.н в это равенство, получим Y=с₁+c₂e^(4х)+х- общее решение неоднородного дифференциального уравнения
найдем первую производную
Y'=(с₁+c₂e^(4х)+х)'=4c₂e^(4х)+1
для нахождения с ₁ и с₂ в задаче Коши подставим начальные условия.
Получим
с₁+c₂e^(4*0)+0=1⇒с₁+c₂=1
4c₂e^(4*0)+1=3⇒c₂=2/4=0.5
зная c₂, найдем с₁=1-c₂=1-0.5=0.5
Значит, частное решение, удовлетворяющее начальным условиям, будет Y=0.5+0.5e^(4х)+х
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Алгебра
-
1)3x-x²=0 2)y²+y=0 3)11x²-x=0 4)9x²+6x=0...
 Avmb13.09.2021 03:43
Avmb13.09.2021 03:43 -
при каком значение b график функции у= bx^2...
 BULATIKSPB17.06.2021 02:15
BULATIKSPB17.06.2021 02:15 -
Найдите координаты точки пересечения без построения графиков функций. Ү— 8Икс...
 Starbiliya200321.10.2022 21:26
Starbiliya200321.10.2022 21:26 -
1. При яких значеннях змінноїх дріб не має змісту? х* -16 А) х = 0; Б) х =...
 murzyatyan05.05.2023 20:58
murzyatyan05.05.2023 20:58 -
5a-3b-(2+5a-3b)=5a+5a-2-3b+3b=2 нужно...
 Allison502.06.2022 23:46
Allison502.06.2022 23:46 -
(9x-3)-6=3 модули с полным решением...
 Kros228volk22523.02.2020 15:47
Kros228volk22523.02.2020 15:47 -
Нужно решение уравнений.-+b)=-c+a-b...
 MilkaV22.12.2020 13:41
MilkaV22.12.2020 13:41 -
Прошу . материальная точка движется прямолинейно по закону s(t)=t^3+2t^2+t(m)....
 tumanovamariam08.04.2023 08:07
tumanovamariam08.04.2023 08:07 -
Выполните действие: 4/25-0.006 2/5: 0,14...
 AZAZA200817.10.2021 12:23
AZAZA200817.10.2021 12:23 -
1)ab=6см, точкаm∈ab. найти bm, если а)am=2bm, б)2am=3bm, в)am/bm=1/5 г)am/bm=3/4...
 vfedkina3503.01.2023 12:25
vfedkina3503.01.2023 12:25

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

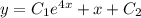 - общее решение
- общее решение 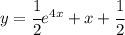 - частное решение
- частное решение