tim152

31.08.2020 06:04

Геометрия

Есть ответ 👍

Найдите меньшую диагональ параллелограмма, стороны которого равны 11 см и 3√3 см, а угол равен 150°.

200

453

Посмотреть ответы 2

Ответы на вопрос:

anastasiagrebep08n1o

Геометрия

4,4(60 оценок)

BD = 7 см

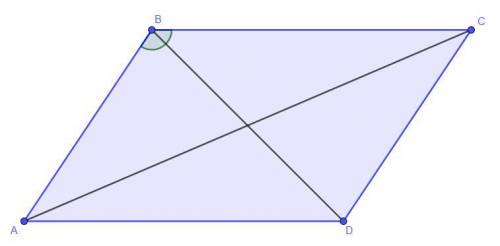
Объяснение:

Дано: AB = $3\sqrt{3}$ см, BC = 11 см, ∠ABC = 150°

Найти: BD - ?

Решение: Рассмотрим треугольник ΔABC. По теореме косинусов:

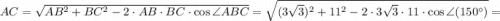
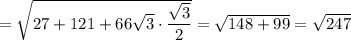$AC = \sqrt{AB^{2} + BC^{2} - 2 \cdot AB \cdot BC \cdot \cos \angle ABC} = \sqrt{(3\sqrt{3} )^{2} + 11^{2} - 2 \cdot 3\sqrt{3} \cdot 11 \cdot \cos \angle (150^{\circ})}=$ $= \sqrt{27 + 121 + 66\sqrt{3} \cdot \dfrac{\sqrt{3} }{2} } = \sqrt{148+99} = \sqrt{247}$ см.

По тождеству параллелограмма:

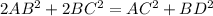
$2AB^{2} + 2BC^{2} = AC^{2} + BD^{2}$

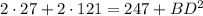
$2 \cdot 27 + 2\cdot 121 = 247 + BD^{2}$

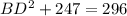
$BD^{2} + 247 = 296$

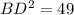
$BD^{2} = 49$

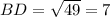$BD = \sqrt{49} = 7$ см.

Найдите меньшую диагональ параллелограмма, стороны которого равны 11 см и 3√3 см, а угол равен 150°.

Lee35

Геометрия

4,6(5 оценок)

по т. пифагора найдем половину основания.треуг. авс, ас основание, вк высота, ак=кс(треугольник равнобедр., высота к основанию является медианой)

ак^2=225-144=81, ak=9, ac=18

s(abc)=9*12=108(площадь треуг.)

r радиус описанной окружности находится по формуле r=(a*b*c)/(4*s)

a,b,c стороны треуг.

r=(15*15*18)/(4*108)=75/8

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.